O rolamento¶
- O rolamento consiste em uma combinação de movimentos de rotação e translação, como por exemplo na roda de um carro/bicicleta.
- Este problema é muito importante em sistemas de transporte
- Vamos considerar o caso mais simples do rolamento, que é o rolamento suave: o objeto não escorrega ou "quica"
Exemplo: roda de uma bicicleta¶
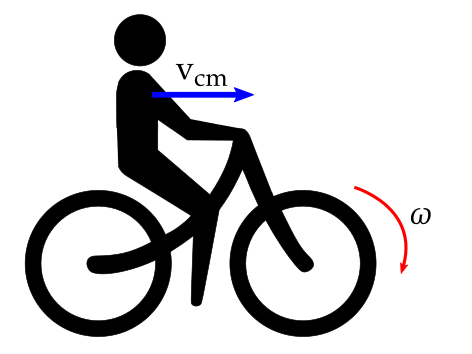
- Como relacionar $\omega$ e $v$?
- Rolamento suave: o perímetro da roda percorre a mesma distância que o centro de massa (C.M.)
Análise do movimento¶
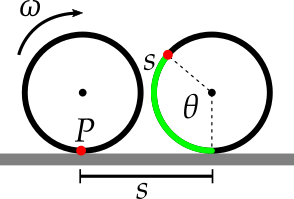
- $s=$ distância percorrida
- $s=$ arco de círculo
- Então, $$s=r\theta$$
- $\frac{ds}{dt} = v_{cm} = r \frac{d\theta}{dt} = r\omega$
- **Rolamento suave:** $$v_{cm}=r\omega$$
Velocidade vetorial¶
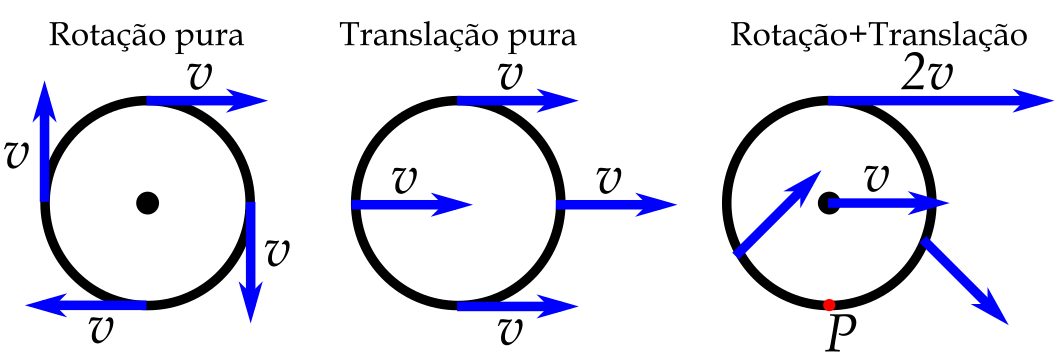
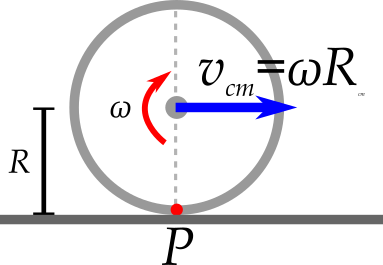
- Percebam que diferentes pontos na periferia da roda possuem velocidades distintas!
- Ponto de contato da roda com o solo tem $v=0$. Por que?
- Ponto mais distante do solo possui $v = 2 v_{cm}$
Rolamento como uma rotação¶
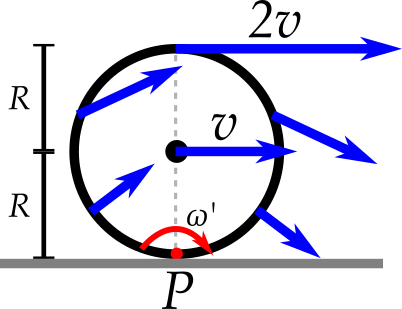
- O rolamento pode ser compreendido como uma rotação em torno do ponto $P$ de contato com o solo
- Neste caso, qual o $\omega'$ associado a esta rotação?
- $\omega'=\omega=v_{cm}/R$ (Observe atentamente o eixo que passa pelo C.M.)
Energia cinética no rolamento¶
- Qual a energia cinética total da roda em movimento?
- En. cinética de rotação + translação!
- $K = K_{rot} + K_{transl}$
- $K = \frac{1}{2}I_{cm}\omega^2 + \frac{1}{2}mv_{cm}^2$
- $K_{rot} = \frac{1}{2}I_{cm}\omega^2$
- $K_{transl} = \frac{1}{2}mv_{cm}^2$
Energia cinética no rolamento¶
- Podemos analisar a energia cinética no rolamento de outra forma complementar, usando o teorema dos eixos paralelos.
- $I=I_{cm}+Mh^2$
- Quem seria $h$ neste caso?
- $h=R$, e $K=\frac{1}{2} I \omega^2$, logo
- $K = \frac{1}{2} I_{cm} \omega^2 + \frac{1}{2} M (R \omega)^2$
- $K = \frac{1}{2}I_{cm}\omega^2 + \frac{1}{2}mv_{cm}^2$
Forças no rolamento¶
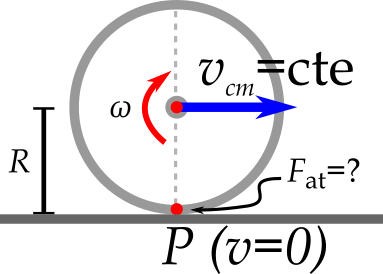
- No rolamento suave com velocidade $v=$cte, não há atrito. O ponto de contato $P$ tem $v=0$.
- Sob aceleração/desaceleração, e sem deslizamento da roda, qual o tipo da força de atrito que atua sobre a roda? Estático ou dinâmico?
- $F_{at}$ estático atua para manter $v=0$ no ponto de contato.
Forças no rolamento¶
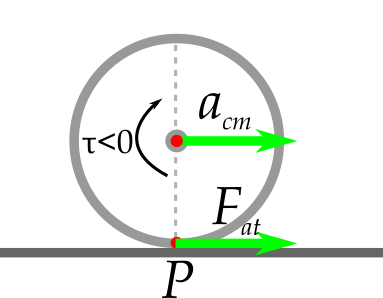
- $v_{cm} = \omega R \rightarrow a_{cm} = \alpha R$
- $F_{at}$ se opõe a mudança de movimento em $P$.
Exemplo: rolamento suave numa rampa¶
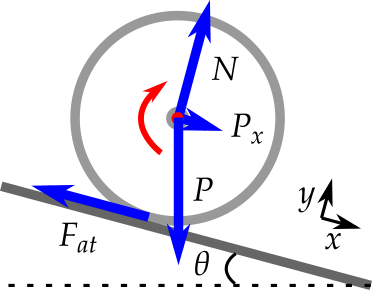
- Que forças atuam sobre o corpo?
- $m g \sin \theta - F_{at} = m a_{cm}$
- $F_{at} = ?$
- $F_{at}$ deve ter um valor suficiente para garantir que o rolamento é suave
- $RF_{at} = I_{cm} \alpha$. $\alpha=?$

- $\alpha=a_{cm}/R$
- $$F_{at} = \frac{I_{cm} a_{cm}}{R^2}$$
- Então, $m g \sin \theta - F_{at} = m a_{cm}$
- $a_{cm} = \frac{g \sin \theta}{1 + \frac{I_{cm}}{MR^2}}$
- Para efeito de comparação, lembrar que um objeto que desce sem rolar num plano sem atrito satisfaz $a_{cm} = g\sin\theta$.
- Qual a velocidade do objeto quando ele parte do repouso e seu centro de massa desce uma altura $h$?
- Notar que $F_{at}$ é estático e atua sobre um ponto onde o objeto está em repouso. $F_{at} . v = 0$
- $W_{Fat} = 0 = \Delta E_m$
- $E_i = m g h$
- $E_f = \frac{1}{2} mv_{cm}^2 + \frac{1}{2} I_{cm}\omega^2$
- $E_f = \frac{1}{2} mv_{cm}^2 + \frac{1}{2} I_{cm}\left(\frac{v_{cm}}{R}\right)^2$
- Usando a conservação de energia, temos
- $E_f = \frac{v_{cm}^2}{2} \left(m + \frac{I_{cm}}{R^2}\right) = m g h$
- $v_{cm}= \sqrt{\frac{2 m g h}{m + \frac{I_{cm}}{R^2}}} = \sqrt{\frac{2 g h}{1 + \frac{I_{cm}}{mR^2}}} $
O ioio¶
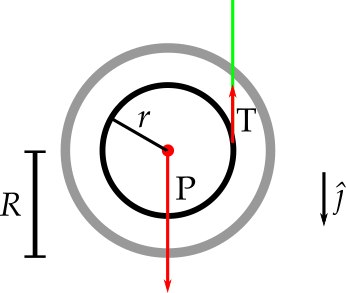
- Seja um ioiô de massa $M$ e momento de inércia $I_{cm}$, qual é a tração na corda?
- Forças: $M a_{cm} = Mg-T$
- Torques: $I_{cm} \alpha = \tau_{res} = T r$
- Aceleração: $a_{cm} = \frac{g}{1+I_{cm}/Mr^2}$
- Tração: $T = \frac{Mg}{1+Mr^2/I_{cm}}$
Torque¶
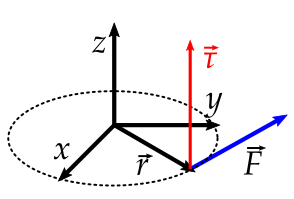
- $\vec{\tau} = \vec{r} \times \vec{F}$
- $\tau = r F \sin \phi$, onde $\phi$ é o ângulo relativo entre $\vec{r}$ e $\vec{F}$

Momento angular¶
- Vimos anteriormente que $\vec{F} = \frac{d\vec{p}}{dt}$, onde $\vec{p}=m\vec{v}$
- Quem seria o análogo de $\vec p$ para movimentos de rotação? (Quantidade de movimento de rotação)
- $\vec \tau = \vec r \times \vec F = \vec r \times \frac{d\vec p}{dt}$
- Supondo $\vec r \approx \vec{\text{cte}}$, teríamos $\vec \tau = \frac{d}{dt}\left(\vec r \times \vec p\right)$
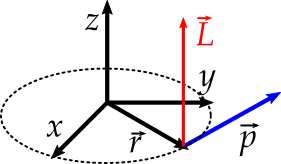
- Momento angular $$\vec L = \vec r \times \vec p,$$ ou ainda $$\vec L = m \vec r \times \vec v $$
Detalhes importantes¶
- Momento angular $$\vec L = \vec r \times \vec p,$$ ou ainda $$\vec L = m \vec r \times \vec v $$
- Notar que mesmo que a partícula não gire em relação à origem, pode-se ter $\vec L \neq \vec 0$!
- Similarmente à $\vec p$, $\vec L$ é conservado num sistema fechado
- Exemplos: MCU e MRU

2ª lei de Newton para rotações¶
- Sabemos que $\vec F = \frac{d\vec p}{dt}$, e gostaríamos de verificar se de fato $\vec{\tau} = \frac{d\vec \ell}{dt}$, onde $\vec \ell$ é o momento angular de uma partícula isolada.
- Em outras palavras, a soma (vetorial) dos torques que agem sobre uma partícula é a taxa de variação do momento angular
Demonstração¶
- $\vec \ell = m \vec r \times \vec v$
- $\frac{d\vec \ell}{dt} = m \frac{d}{dt}\left(\vec r \times \vec v\right)$
- $= m \left(\frac{d\vec r}{dt} \times \vec v + \vec r \times \frac{d \vec v}{dt}\right)$
- Mas $\frac{d\vec r}{dt} \times \vec v = \vec v \times \vec v = 0$, logo
- $\frac{d\vec \ell}{dt} = m \vec r \times \frac{d \vec v}{dt}$, ou ainda $ \frac{d\vec \ell}{dt} = \vec r \times \vec F_R$, onde $\vec F_R = \sum_i \vec F_i$ é a força resultante que atua sobre o objeto.
- Seja $\vec \tau_{res}$ o torque associado à força resultante, $$\vec\tau_{res}=\frac{d\vec \ell}{dt}$$
Momento angular de um sistema de partículas¶
- Seja o momento angular total $\vec L = \vec \ell_1 + \vec \ell_2+ \vec \ell_3+\dots+\vec \ell_n = \sum_{i=1}^n \vec \ell_i$
- $\frac{d\vec L}{dt}=\sum_{i=1}^n \frac{d\vec\ell_i}{dt} = \sum_{i=1}^n \vec\tau_{i,res}$
- onde $\vec\tau_{i,res}$ é o torque resultante que atua sobre a partícula $i$
- Lembrando que forças internas formam pares ação-reação, podemos simplificar a soma acima de forma similar ao que fizemos anteriormente para movimentos de translação
- $\frac{d\vec L}{dt}= \sum_{i=1}^n \vec\tau_{i,ext} = \vec{\tau}_{ext}$
- O momento angular total de um sistema de partículas só varia no tempo sob a ação de torques associados à forças externas apenas
Momento angular de um sistema de partículas¶
- $\frac{d\vec L}{dt}= \sum_{i=1}^n \vec\tau_{i,ext} = \vec{\tau}_{ext}$
- O momento angular total de um sistema de partículas só varia no tempo sob a ação de torques associados à forças externas apenas.
- O torque externo resultante, $\vec{\tau}_{ext}$, é igual à taxa de variação do momento angular do sistema $\vec L$.
- Relação análoga a $\vec F_R = \frac{d\vec P}{dt}$
Corpo rígido girando em torno de um eixo fixo¶
- Qual o momento angular de um corpo rígido que gira em torno de um eixo fixo?
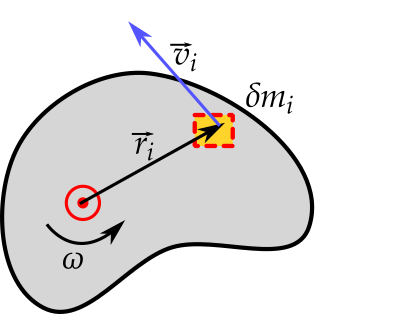
- Em termos de escalares, $L = \sum_{i=1}^n \ell_i = \sum_{i=1}^n \delta m_i r_i v_i$
- Mas $v_i = r_i \omega$, e $L = \sum_{i=1}^n \delta m_i r_i^2 \omega$, ou $$L = I \omega$$
- onde $I = \sum_{i=1}^n \delta m_i r_i^2 = \int r^2 dm$ é o momento de inércia
- Vetorialmente, podemos afirmar também que $$\vec L = I \vec \omega$$ (lembrar de $\vec p = m \vec v$!)
Exemplo¶
Um barbante realiza uma força $\vec F$ sobre um disco, um anel e uma esfera. Todos possuem a mesma massa e raio, e estão inicialmente em repouso. Ordene crescentemente (a) o momento angular dos objetos num tempo $t>0$ e (b) o módulo das suas respectivas velocidades angulares.
Dados: $I_{cm, disco} = \frac{1}{2}MR^2, I_{cm, anel} = MR^2, I_{cm, esfera} = \frac{2}{5}MR^2$
R.: (a) $L_{esfera}=L_{Disco}=L_{Anel}$; (b) $|\omega_{Anel}|$<$|\omega_{Disco}|$<$|\omega_{esfera}|$
Mais correspondências entre o movimento de rotação e o de translação¶
| Var. do movim. | Momento | Momento total | Var. resultante do movim. | Lei de conserv. | |
|---|---|---|---|---|---|
| Translação | $\vec{F}$ | $\vec{p}$ | $\vec{P}=\sum_i\,m_iv_i=M\vec{v_{cm}}$ | $\vec{F}_{res}=\frac{d\vec p}{dt}$ | $\vec{P}=\vec{\text{cte}}$ |
| Rotação | $\vec{L}$ | $\vec{\ell}$ | $\vec{L}=\sum_i\,\ell_i=I\vec{\omega}$ | $\vec{\tau}_{res}=\frac{d\vec\ell}{dt}$ | $\vec{L}=\vec{\text{cte}}$ |
Conservação do momento angular¶
- Na ausência de torques $\vec\tau$ externos, $$\vec L = \vec{\text{cte}}$$
- Se $\frac{d\vec L}{dt}=0$, então $$ \vec L_i = \vec L_f = \vec{\text{cte}}$$ para um sistema isolado
- Se a soma dos torques que atuam sobre um sistema é nulo, o momento angular é constante


