Configurações

Tópico 7 - Trabalho e energia

Anderson M Amaral - amamaral.github.io/teaching

Trabalho e energia

Fundamentos da Física, Capítulo 7 e 8

Leituras complementares:

• Nussenzveig - Capítulos 6 e 7
• Feynman, Leighton, Sands - Capítulos 4, 13 e 14

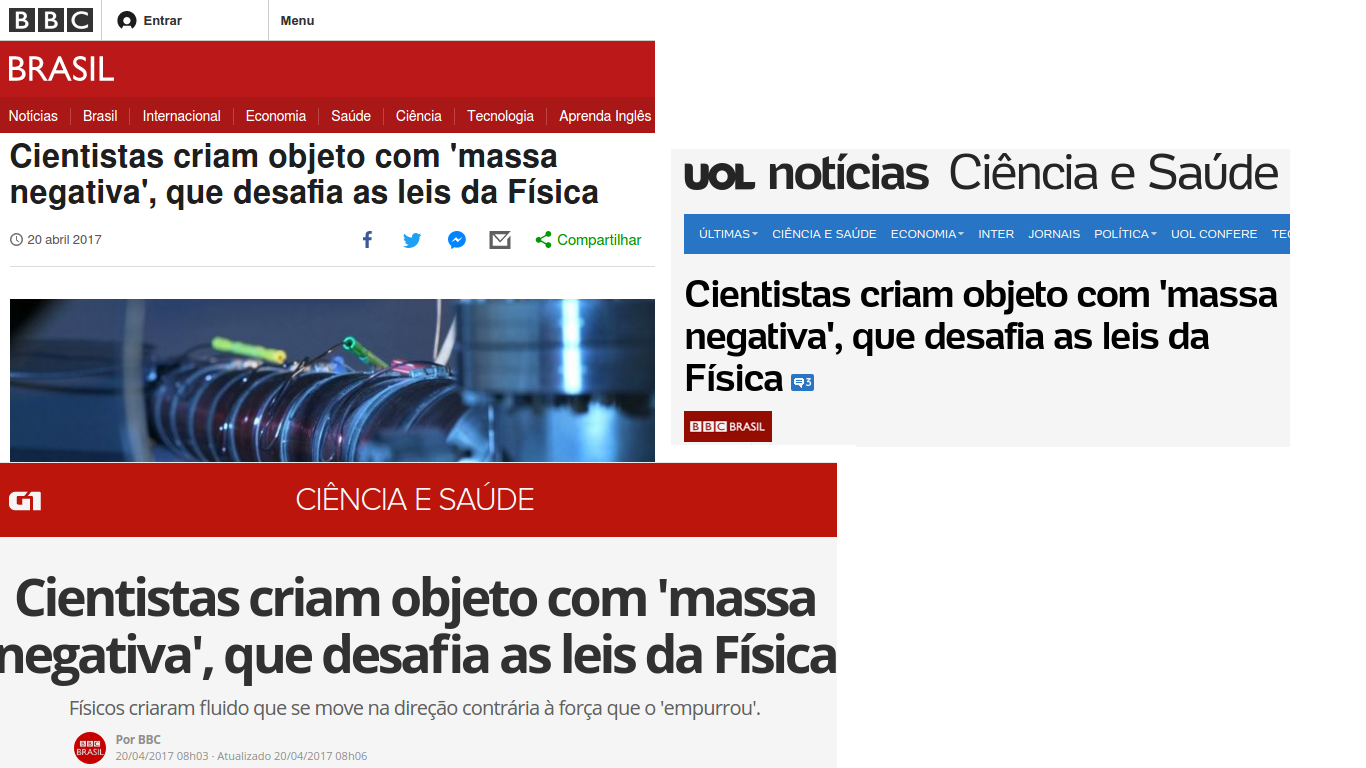
Pêndulo simples

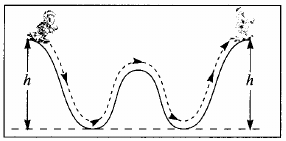
• Massa lançada de A, sem atritos. Após um tempo $T$, a massa está em $B$.
• Por quê o pêndulo sobe quando está no ponto B? $\vec{P}$ não aponta para baixo?
• Existe alguma propriedade que está relacionado com a velocidade não nula no ponto $B$.
• Notar que, após $2T$, a partícula está em $C$, que possui a mesma altura de $A$.
• A trajetória depois será C-B-A.
• Existe alguma propriedade que é independente da direção e sentido de $\vec{v}$!

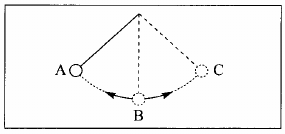
Objeto em movimento vertical

• Massa $m$, velocidade inicial $\vec{v}_0$ para baixo.
• $$v^2=v_0^2+2a\Delta z = v_0^2+2ah$$
• A expressão acima pode explicar a propriedade anterior?
• Obs.: $v^2$ não depende da direção de $\vec{v}$. Lembre que $v^2=\vec{v}\cdot\vec{v}$.
• Se a massa $m$ sofre uma colisão perfeitamente elástica (colisão ideal), o objeto retornará a altura inicial $h$.

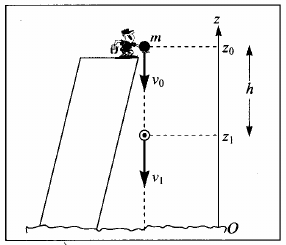
Objeto descendo em um plano inclinado

• Torricelli: $v^2=v_0^2+2al$. $a=?$
• $a = g \sin\theta$
• $v^2=v_0^2+2g \sin \theta\, l$
• mas $l \sin \theta$ = $h$ é o deslocamento ao longo da direção vertical, logo
• $$v^2=v_0^2+2 g h.$$
• Em termos de $h$, encontramos uma expressão idêntica ao caso da queda vertical...
• Podemos pensar numa relação entre a posição e $v$ para cada ponto da trajetória?Massa $m$, velocidade inicial $\vec{v}_0$ para baixo.

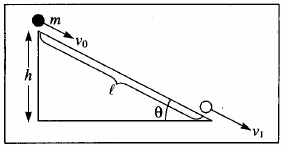
Relação entre $v$ e $z$

• Definindo $h = z_0-z$,
• $v^2=v_0^2+2 g h = v_0^2+2 g (z_0-z).$
• Passando $2gz$ para o lado esquerdo, $$v^2 + 2gz=v_0^2+ 2 g z_0=\text{cte}.$$
• Para todos os pontos na trajetória de uma partícula sob ação do campo gravitacional nas imediações da superfície, a quantidade acima é conservada.
• Notar que, uma constante pode ser multiplicada por qualquer outra constante $C$ (não nula), e ainda assim será uma constante, de forma que $$C(v^2 + 2gz)=cte$$ também é conservado!
• Os exemplos mencionados de queda livre possuem dinâmicas que independem da massa... $C$ pode ser função de $m$

Determinação de $C$

• $C(v^2 + 2gz)=cte$. Para determinar $C$, precisamos de uma dinâmica que dependa da massa.
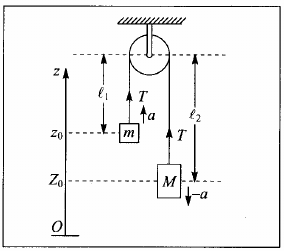
• Máquina de Atwood.
• Quantidade conservada: $$\sum_\text{partículas}\left(\frac{mv^2}{2} + mgz\right)=E=cte.$$
• $C=\frac{m}{2}$, e $E$ é a energia mecânica do sistema.

Outras constantes?

• Até agora, foi mencionado apenas o caso de uma possível constante multiplicativa
• E constantes aditivas? cte + cte = cte, e $\frac{mv^2}{2} + mgz + D = E'$ também não muda durante o movimento!
• Constantes aditivas são irrelevantes. Neste exemplo, uma mudança da origem varia a constante aditiva.
• E outras operações matemáticas? Ex.: $\left(\frac{mv^2}{2} + mgz + D\right)^r=cte$...(?)
• No caso Newtoniano, veremos a seguir que há apenas constantes aditivas.
• Relatividade restrita: $E=\sqrt{(mvc)^2 + (mc^2)^2}=cte$

Trabalho e energia: bate-estacas

• Bloco de massa $m$ solto a partir do repouso em $z_0$, colide com a estaca em $z=0$.
• Energia ao soltar o bloco: $E = mgz_0$.
• Energia imediatamente antes de colidir com a estaca: $E = \frac{mv^2}{2}$.
• Aprox.: supor que a força impulsiva $F$ do impacto produz uma aceleração $a$ constante. ($a<0$)
• Aprox. 2: outras forças são desprezíveis durante a ação de $F$.
• Eq. de mov. do bloco: $-F=ma$.
• Desaceleração do bloco até o repouso: $v^2=-2a\Delta z$
• Ou seja, $E = \frac{mv^2}{2} = F \cdot \Delta z$

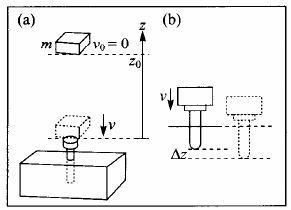
Trabalho e energia

• $E = \frac{mv^2}{2} = F \cdot \Delta z$.
• Unidade de energia $E\longrightarrow$ kg m$^2$/s$^2$ N $\cdot$ m = 1 J (Joule).
• "A força $F$ aplicada à estaca, enterrando-a de $\Delta z$, ou seja, produzindo um deslocamento de $\Delta z$ na direção da força, realiza um trabalho $$\Delta W = F \cdot \Delta z$$ sobre a estaca."
• A energia representa a capacidade de realizar trabalho. Um objeto que realiza trabalho, transfere sua energia para outro.
• Há vários tipos de energia. Em mecânica, temos p. ex.:
• Energia cinética: $K=\frac{mv^2}{2}$. Energia associada ao movimento.
• Energia potencial gravitacional: $U=mgz$. Energia potencialmente disponível devido à $\vec{g}$.

Trabalho e energia

• No caso de um corpo em queda livre
• $E = \frac{mv^2}{2} + m g z = K + U$.
• Energia cinética: $K=\frac{mv^2}{2}$. Energia associada ao movimento.
• Energia potencial gravitacional: $U=mgz$. Energia potencialmente disponível devido à $\vec{g}$.
• Durante o movimento, K se transforma em U, ou vice-versa.
• Ex.:

Trabalho e energia

• A realização de trabalho sobre um objeto modifica sua energia
• Supor energia inicial $E_1 = \frac{mv_1^2}{2}$
• A força $F$ realiza um trabalho $W_F = F\cdot(x_2-x_1)$ entre $x_1$ e $x_2$
• Então, $E_2 = E_1 + W_F$, ou $$\frac{mv_2^2}{2}=\frac{mv_1^2}{2}+F\cdot(x_2-x_1)$$

Trabalho de uma força variável

• Se $F$ varia, podemos aproximar o trabalho em pequenos deslocamentos como sendo $$\Delta W = W_F = F(x_i)\Delta x$$
• Somando o trabalho realizado em vários segmentos $W_F = \sum_i F(x_i)\Delta x$.
• Tomando segmentos arbitrariamente pequenos ($\lim \Delta x\rightarrow 0$), $$W_F = \int_{x_0}^{x_1} F(x)\;dx.$$

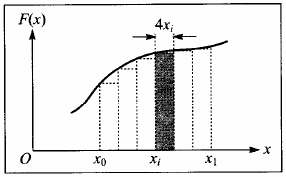
• Integral $\rightarrow$ Área entre a curva e o eixo $x$.

Aplicação à lei de Hooke

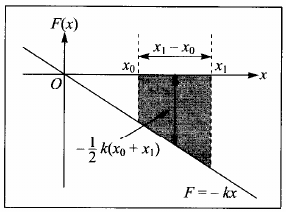
• Para uma mola ideal, $F = - k x$
• $W = - \int_{x_0}^{x_1} k x\;dx.$
• Graficamente, $\int_{x_0}^{x_1} x\;dx = \frac{-k}{2}(x_0+x_1)(x_1-x_0).$
• Ou seja, $W = - \frac{k}{2} (x_1^2-x_0^2)$.
• Trabalho sobre a partícula é negativo se a deformação na mola aumenta.

Trabalho e energia para uma força variável

• Qual a relação entre trabalho e energia para uma força variável?
• Em uma dimensão, $F=ma=m\frac{dv}{dt}$,
• $W_{x_0\rightarrow x_1}=\int_{x_0}^{x_1} m\frac{dv}{dt} dx$
• Mas, $\frac{dv}{dt} dx = \frac{dv}{dt} \frac{dx}{dt} dt$, e
• $W_{x_0\rightarrow x_1}=\int_{t_0}^{t_1} mv \frac{dv}{dt} dt$
• [Note a mudança no intervalo de integração: $x_0=x(t_0)$, e $x_1=x(t_1)$].
• Perceba que $\frac{d}{dt}\frac{v^2}{2} = v \frac{dv}{dt}$. Ou seja, o integrando é a derivada de $v^2/2$
• $W_{x_0\rightarrow x_1}= \frac{mv_1^2}{2}-\frac{mv_0^2}{2}=\Delta K$
• O trabalho realizado é igual a variação da energia cinética, para qualquer força.
• Comentário: observe que o fator $\frac{1}{2}$ 'colocado com a mão' na determinação da constante multiplicativa por meio do experimento da máquina de Atwood aparece aqui naturalmente.

Conservação da energia mecânica em uma dimensão

• Exemplo: queda livre
• $W_{z_0\rightarrow z_1} = \int_{z_0}^{z_1} (-mg) dz$
• $W_{z_0\rightarrow z_1} = -mg(z_1-z_0) = - (U_1-U_0) = \Delta U$,
• onde $U=mgz$ é a energia potencial gravitacional.
• Recordando que $W_{z_0\rightarrow z_1}$ é a variação da energia cinética, $\Delta K$, $\Delta K = - \Delta U$, ou $$\Delta T+\Delta U = \Delta(T+U)=\Delta E = 0.$$
• A energia mecânica total do sistema, $E=T+U$, não varia durante o movimento. $E$ é conservada na queda livre.

Conservação da energia mecânica

• Exemplo: sistema massa-mola
• Anteriormente vimos: $$W_{x_0\rightarrow x_1} = - \frac{k}{2} (x_1^2-x_0^2).$$
• Podemos reescrever como $$W_{x_0\rightarrow x_1}=-[U(x_1)-U(x_0)]$$
• Energia potencial: $$U(x)=\frac{1}{2}kx^2$$
• Energia mecânica total: $$E=K+U=\frac{1}{2}mv^2+\frac{1}{2}kx^2$$
• Quando for possível escrever $W_{x_0\rightarrow x_1}=-[U(x_1)-U(x_0)],$ a força é conservativa.
• Em forças conservativas, a energia potencial depende apenas da posição. Ex.: peso e mola ideal.

Forças conservativas

• Supor que a força que atua depende apenas da posição. $F = F(x).$
• Fixando a posição inicial $x_0$, podemos definir $$\Phi(x)=\int_{x_0}^{x}F(u)du=W_{x_0\rightarrow x}.$$
• Notar que $$\Phi(x_2)-\Phi(x_1)=\int_{x_0}^{x_2}F(u)du-\int_{x_0}^{x_1}F(u)du,$$
• mas as integrais satisfazem as propriedades $\int_a^b=-\int_b^a$, e $\int_a^c+\int_c^b=\int_a^b$, tal que
• $$\Phi(x_2)-\Phi(x_1)=\int_{x_1}^{x_2}F(u)du=W_{x_0\rightarrow x_1},$$ e a energia potencial associada é $$ U(x)=-\Phi(x)=-\int_{x_0}^{x}F(u)du.$$

Relação entre forças conservativas e o potencial

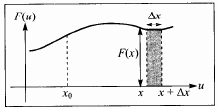
• $\Phi$ para pequenas variações na posição
• $\Delta \Phi = \Phi(x+\Delta x)-\Phi(x)$
• $\Phi(x+\Delta x)-\Phi(x)\approx F(x) \Delta x$
• $\frac{\Delta \Phi}{\Delta x} = F(x)$
• Tomando $\Delta x \rightarrow 0$,
• $$\frac{d\Phi}{dx}=F(x),$$
• ou ainda, $$F(x) = -\frac{d U(x)}{dx}.$$

• A força é menos a derivada da energia potencial

Dois exemplos simples:

• Massa-mola: $U=\frac{1}{2}kx^2$
• $F = -\frac{dU}{dx} = - k x$

• Aceleração gravitacional: $U=mgz$
• $F = -\frac{dU}{dx} = - mg$

Consequência importante

• Trabalho realizado entre $x_0$ e $x_1$: $$\int_{x_0}^{x_1}F(x)dx=W_{x_0\rightarrow x_1}=U_0-U_1.$$.
• Trabalho realizado no sentido inverso ($x_1$ para $x_0$): $$\int_{x_1}^{x_0}F(x)dx=W_{x_1\rightarrow x_0}=U_1-U_0.$$
• Somando membro a membro, $$W_{x_0\rightarrow x_1}+W_{x_1\rightarrow x_0}=0$$
• O trabalho total realizado quando uma partícula volta ao ponto inicial é nulo para uma força conservativa.
• Notar que forças de atrito não satisfazem esta condição!
• $F_{at}$ tem sempre sentido oposto ao movimento. $F_{at}$ não é conservativa!

Movimento sob forças conservativas: alguns aspectos qualitativos

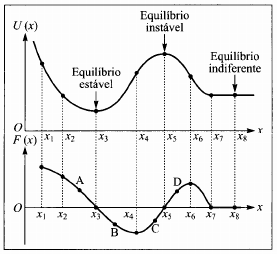
• Ponto de equilíbrio: $F(x)=0$
• Lembrar que $F(x)=-\frac{dU}{dx}$
• Se a concavidade de $U$ é para cima: equilíbrio estável
• Se a concavidade de $U$ é para baixo: equilíbrio instável
• Se $U$ é constante, não há concavidade nem força. Equilíbrio indiferente.

Movimento sob forças conservativas: alguns aspectos qualitativos

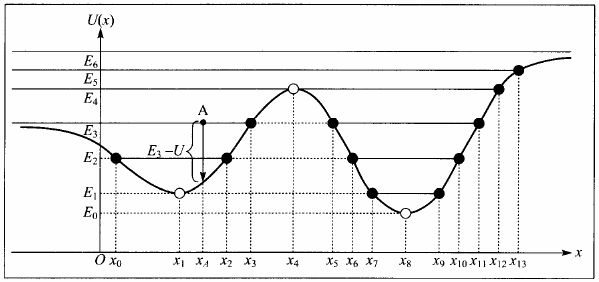
• $E=\frac{1}{2} mv^2 + U = \text{cte}$
• $mv^2\geq 0$ implica que $E\geq U(x)$ onde o movimento é permitido.
• Para qualquer $x$, $v(x)=\pm\sqrt{\frac{2}{m}[E-U(x)]}$
• Pontos de retorno: $v(x)=0$ quando $U(x)=E$

Exemplo (M. Copelli) Um bloco de massa $m$ desce ao longo de um plano inclinado sem atrito (vide figura). Ele prende-se então a uma mola de constante elástica $k$, que é comprimida até o bloco parar momentaneamente. Neste processo, a variação da energia potencial gravitacional é:

1. positiva
2. negativa
3. nula
4. não é possível determinar

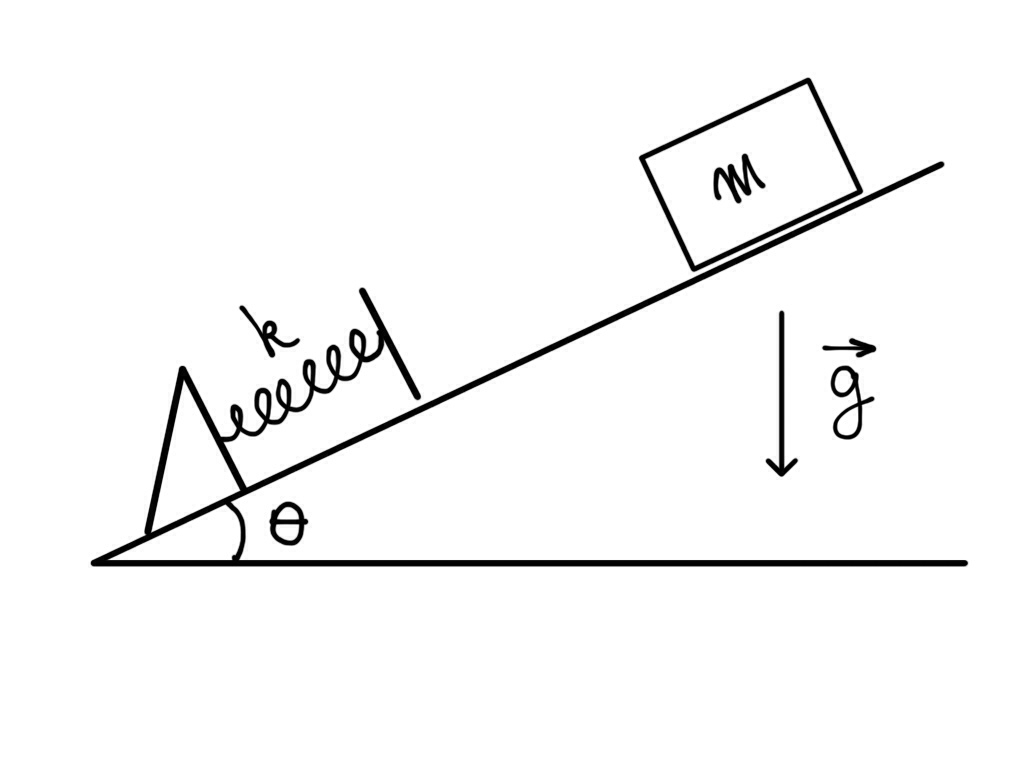
Exemplo (M. Copelli) Um bloco de massa $m$ desce ao longo de um plano inclinado sem atrito (vide figura). Ele prende-se então a uma mola de constante elástica $k$, que é comprimida até o bloco parar momentaneamente. Neste processo, a variação da energia potencial elástica é:

1. positiva
2. negativa
3. nula
4. não é possível determinar

Exemplo (M. Copelli) Um bloco de massa $m$ desce ao longo de um plano inclinado (vide figura). Ele prende-se então a uma mola de constante elástica $k$, que é comprimida até o bloco parar momentaneamente. Suponha agora que este processo ocorra na presença de atrito entre o bloco e o plano inclinado. Neste caso, ainda é possível definir uma energia potencial gravitacional e uma energia potencial elástica para o problema?

1. Sim
2. Não
3. Depende
4. Veja bem...

Exemplo (M. Copelli) Uma partícula move-se ao longo de um eixo horizontal $x$ sujeito à ação de uma única força conservativa $F$. A energia potencial $U$ associada a esta força é mostrada na figura como função da posição $x$. Quando a partícula se desloca de $x_1$ até $x_2$, o trabalho realizado por $F$ é:

1. 15 J
2. -15 J
3. 20 J
4. Não há dados suficientes

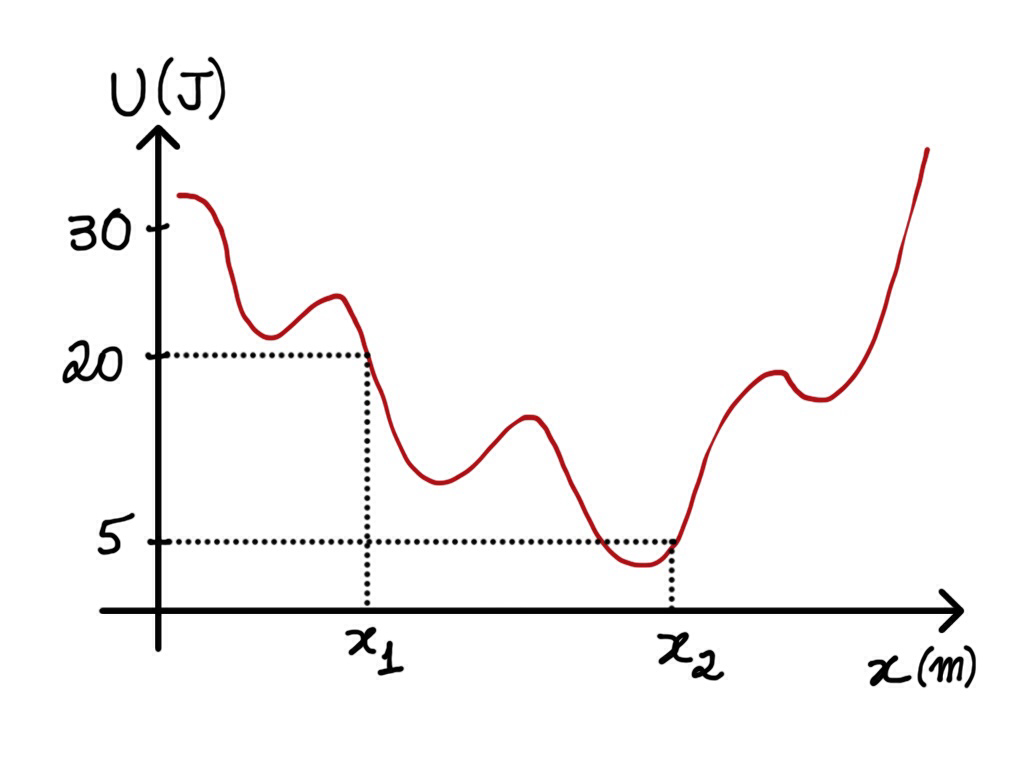
Exemplo (M. Copelli) Uma partícula move-se ao longo de um eixo horizontal $x$ sujeito à ação de uma única força conservativa $F$. A energia potencial $U$ associada a esta força é mostrada na figura como função da posição $x$. Quando a partícula se encontra em $x_1$, a força $F$ é:

1. positiva
2. negativa
3. nula
4. não há dados suficientes

Problema 7.38 (9ª Ed.) Um bloco de 1,5 kg está em repouso sobre uma superfície horizontal sem atrito quando uma força ao longo de um eixo $x$ é aplicada ao bloco. A força é dada por $\vec{F}(x) = (2, 5 - x^2 )\hat{i}$ N, onde $x$ está em metros e a posição inicial do bloco é $x = 0$.

• (a) Qual é a energia cinética do bloco ao passar pelo ponto $x = 2,0$ m?
• (b) Qual é a energia cinética máxima do bloco entre $x = 0$ e $x = 2,0$ m?

R.: (a) $E_c = \frac{7}{3} J \approx 2,3 J$ (b) É max. em $x=\sqrt{2,5}$. $E_c^{max} = 2,5 \sqrt{2,5} - 2,5^{3/2}/3\approx 2,5 J$

Exemplo: Potencial de Lennard-Jones

• Modelo para interação entre 2 átomos em molécula diatômica
• Consideramos 1 átomo na origem, e o potencial $U$ na direção do outro.
• $U(x) = D \left[\frac{a^{12}}{x^{12}}-2\frac{a^6}{x^6}\right]$
• $F(x) = -\frac{dU}{dx} = 12 \frac{D}{a} \left[\frac{a^{13}}{x^{13}}-\frac{a^7}{x^7}\right]$
• Notar que $F(a)=0$ (posição de equilíbrio)

x = linspace(0.75, 2, 100)

U = 1 * ( 1/x**12 - 2 * 1/x**6 )

xlim(x[0],x[-1])
xticks([x[13], 1.0, x[38]], ['$x_1$', 'a', '$x_2$'])
xlabel("x")
hlines(0, x[0], x[-1])

ylim(-1.5,1.5)
yticks([-1, U[13], 0], ['-D', 'E', 0])
ylabel('U(x)')

hlines(-1, 0,     1, linestyles='--')
vlines(1 , -1.5, -1, linestyles='--')

hlines(U[13], 0,     x[38], linestyles='--')
vlines(x[13] , -1.5, U[13], linestyles='--')
vlines(x[38] , -1.5, U[13], linestyles='--')

plot([x[13], 1, x[38]], [U[13], -1, U[13]], 'o')

#grid()

plot(x, U)
title("Potencial de Lennard-Jones");

Breve comentário

Alguém viu as notícias abaixo?

Enquanto isso, no mundo científico...

• As leis de Newton e tudo o que dissemos até agora continua válido
• Massa é sempre positiva.

Alguns conceitos sobre integrais

• A integral $I = \int_{x_0}^{x_1} f(x) \,dx$ representa a área entre a curva $f(x)$ e o eixo $x$ quando $x$ varia no intervalo entre $[x_0, x_1]$.
• Subdividindo o intervalo $[x_0, x_1]$ em $N$ segmentos, $I \approx \sum_{i=1}^N F(x_i)\Delta x$.
• Tomando segmentos arbitrariamente pequenos ($\lim \Delta x\rightarrow 0$), $$I = \int_{x_0}^{x_1} F(x)\;dx.$$

• Integral $\rightarrow$ Área entre a curva e o eixo $x$.

Alguns conceitos sobre integrais

• $I(x) = \int_{x_0}^{x} F(x)\;dx.$

• Qual a taxa de variação de $I(x)$ em função de $x$ $\left( \frac{dI}{dx}\right)$?
• $I(x) \approx \sum_{i=1}^N F(x_i)\Delta x$
• $I(x+\Delta x) \approx \sum_{i=1}^N F(x_i)\Delta x + F(x)\Delta x$
• $I(x+\Delta x) - I(x) \approx F(x)\Delta x$
• $\frac{I(x+\Delta x) - I(x)}{\Delta x} \approx F(x)$. No limite $\Delta x \rightarrow 0$, $$ \frac{dI(x)}{dx} = F(x)$$

Integrais indefinidas (guia rápido)

• Então, $I(x) = \int_{x_0}^{x} F(x)\;dx$, e $F(x) = \frac{dI(x)}{dx}$.
• A derivada da primitiva $I(x)$ é o integrando $F(x)$ (ver o Teorema Fundamental do Cálculo - TFC)
• Se $C$ é constante, $F(x) = \frac{d}{dx}I(x) = \frac{d}{dx}[I(x)+C]$
• Na prática, para resolver integrais buscaremos funções $I(x)$ tal que a derivada seja $F(x)$.
• Ex.: monômio $x^i$. Como resolver $\int x^i dx$?
• Recordando que $\frac{d(x^n)}{dx} = n x^{n-1}$, se $i=n-1$, temos que $$x^i = \frac{d}{dx}\left(\frac{x^{i+1}}{i+1}\right),$$ exceto para $i=-1$
• Usando o TFC, $$\int x^i dx = \frac{x^{i+1}}{i+1} + C,\text{ contanto que }i\neq-1$$ onde devemos adicionar a constante do lado direito no caso mais geral.

Integral definida (guia rápido)

• $A = \int_a^b x\,dx \rightarrow $ área entre a curva $y=x$ e o eixo $x$, quando $x$ varia no intervalo $[a,b]$
• Área: $A = \frac{(a + b)(b-a)}{2} = \frac{b^2}{2} - \frac{a^2}{2}$
• Do slide anterior, $I(x) = \int x\,dx = \frac{x^2}{2} + C$, tal que podemos representar $ A = I(b)-I(a)$
• Em geral, dada qualquer primitiva $I(x)=\int f(x)dx$, então $$\int_a^b f(x)dx = I(b)-I(a)$$
• Ex.: $\int_0^1 x^2\,dx = \left.\frac{x^3}{3}\right|_{x=0}^1 = \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3}$

Algumas regras de integração

Sejam $f(t)$ e $g(t)$ duas funções quaisquer* e $c=cte$,

• $\int_a^b cf(x)\,dx = c \int_a^b f(x)\,dx$
• $\int_a^b [f(x)\pm g(x)]dx = \int_a^b f(x)dx\pm\int_a^b g(x)dx$
• $\int_a^b f(x)\,dx = -\int_b^a f(x)\,dx$

• $\int_a^b x^i dx = \frac{b^{i+1}-a^{i+1}}{i+1} + C$ (desde que $i\neq-1$)
• $\int_a^b x^{-1} dx = \log|b| - \log|a|$

Trabalho em 2D e 3D

• Nas últimas aulas, discutimos principalmente a relação entre trabalho e energia em sistemas unidimensionais.
• Como adicionar as outras dimensões espaciais?
• Voltemos ao caso de uma força $\vec{F}$ constante
• Ao longo do plano, o bloco está sujeito a um deslocamento $\vec{l}$
• Variação de velocidade do bloco: $v^2 - v_0^2 = 2 a l = 2 \frac{F}{m} \cos\theta l$
• Trabalho realizado pela força: $W = F \cos\theta\,l$

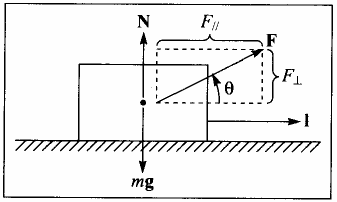
• Trabalho realizado pela força: $W = F \cos\theta\,l$, ou
• $$W = F_\parallel l = \vec{F}\cdot\vec{l}$$
• O trabalho realizado por uma força $\vec{F}$ sobre uma partícula que sofre um deslocamento $\vec{l}$ é o produto escalar entre $\vec{F}$ e $\vec{l}$.
• Forças perpendiculares ao deslocamento não realizam trabalho!

Trabalho para uma força geral

• A força $\vec{F}$ pode ser diferente em cada posição do espaço: $$\vec{F}=\vec{F}(x,y,z)$$
• Como calcular o trabalho quando a força é vetorial?
• Trabalho devido à um pequeno deslocamento: $W = \vec{F} \cdot \Delta\vec{l}$, onde $\Delta\vec{l}$ é um pequeno deslocamento.
• Trabalho total numa trajetória: $W \approx \sum_{i=1}^N\vec{F} \cdot \Delta\vec{l}_i$, onde $\Delta\vec{l}_i$ é um pequeno deslocamento.
• No limite $\Delta\vec{l}\rightarrow 0$, o trabalho é dado pela integral de linha (Cálc. 3!) $$W = \int_i^f \vec{F} \cdot d\vec{l}$$
• Força $\vec{F}$ é conservativa se $W = \int_i^f \vec{F} \cdot d\vec{l}$ depende apenas dos pontos final e inicial, $f$ e $i$, e não da trajetória específica entre $i$ e $f$.

Energia cinética em 3D

• Em 1D, temos $K = \frac{mv_x^2}{2}$. O que ocorre em duas ou três dimensões?
• Podemos separar a 2ª Lei de Newton em cada direção $$\vec{F}=m\frac{d\vec{v}}{dt}\rightarrow\begin{cases} F_{x}=m\frac{dv_{x}}{dt}\\ F_{y}=m\frac{dv_{y}}{dt}\\ F_{z}=m\frac{dv_{z}}{dt} \end{cases}$$
• Trabalho associado às forças resultantes em cada direção espacial pode ser calculado de forma independente
• Então, $$K = \frac{mv_x^2}{2}+\frac{mv_y^2}{2} + \frac{mv_z^2}{2} = \frac{mv^2}{2}$$

Sistemas dissipativos

• Em sistemas físicos reais, sempre existe dissipação. O que acontece com a energia nesses casos?
• Suponha um bloco de massa $m$ e velocidade inicial $v_i$ sobre um plano horizontal, unicamente sob ação do atrito.
• Energia inicial: $E = \frac{1}{2} mv_i^2$
• Força de atrito: $F_{at} = -\mu_c m g$
• Trabalho devido à $F_{at}$ num deslocamento $d>0$: $W_{at} = -\mu_c m g d < 0$
• Se $F_{at}=F_R$, então $W_{at}$ é a variação da energia cinética: $ \Delta K = \frac{1}{2} mv_f^2 - \frac{1}{2} mv_i^2 = W_{at} $, ou $$ E = \frac{1}{2} mv_i^2 = \frac{1}{2} mv_f^2 - W_{at} $$
• Energia dissipada pelo atrito: $\Delta E = - W_{at} = \mu_c m g d > 0 $

Potência

• Até aqui, falamos apenas do trabalho realizado, independentemente do tempo para a realização do deslocamento
• Potência $P$ indica quão rápido pode-se realizar trabalho.
• Potência média: $$\bar{P} = \frac{W}{\Delta t}.$$
• Potência instantânea: $$P = \frac{dW}{dt}.$$ ($dW$ é o trabalho infinitesimal realizado num tempo $dt$)
• $dW = \vec{F}\cdot d\vec{s}$, e $$P = \frac{\vec{F}\cdot d\vec{s}}{dt} = \vec{F}\cdot\vec{v}.$$
• Se $P=\bar{P}=cte$, então $$W = P \Delta t.$$
• Unidade de potência: J/s = W (Não confundir Watts com trabalho!)

• Vale notar que, dada uma força geral, temos que o trabalho associado satisfaz
• $\frac{dW}{dt} = P$, ou seja $$W = \int_{t_0}^{t_1} P(t) dt,$$ e o trabalho realizado pela força entre os tempos $t_1$ e $t_2$ equivale à área entre $P(t)$ e o eixo horizontal.
• Em particular, para a força resultante: $$P_R = \frac{dW_R}{dt}\text{, ou } W_R=\int_{t_0}^{t_1} P_R(t) dt$$
• Como o trabalho da força resultante $W_R$ fornece a variação da energia cinética $\Delta K$, afirmamos que $$ \Delta K=\int_{t_0}^{t_1} P_R(t) dt$$