Tópico 8 - Centro de massa, momento linear e colisões

Anderson M Amaral - amamaral.github.io/teaching

Centro de massa, momento linear e colisões

Fundamentos da Física, Capítulo 9

Leituras complementares:

  • Nussenzveig - Capítulo 8
  • Feynman, Leighton, Sands - Capítulos 4, 13 e 14

Recapitulando...

  • Observação das características do movimento $\rightarrow$ Cinemática
  • Formulação das leis que regem as causas do movimento $\rightarrow$ Leis de Newton.
  • Trabalho e energia. Conservação da energia.
  • Até agora, analisamos apenas a dinâmica de uma única partícula pontual.
  • O que acontece com mais de uma partícula? Ou um objeto não pontual?

Centro de massa (C.M.)

  • É um ponto especial, move-se como se toda a massa do sistema estivesse concentrada neste ponto.
  • Ex.: 2 partículas, massas $m_1, m_2$ e posições $x_1, x_2$.
  • $x_{cm} = \frac{m_1 x_1 + m_2 x_2}{m_1+m_2} = \frac{1}{M}(m_1 x_1 + m_2 x_2)$
  • $x_{cm}$: Posição média, ponderada pelas massas. $M$: Massa total.
  • Muitas massas: $x_{cm} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3 + \dots}{m_1+m_2+m_3+\dots} = \frac{\sum_{i=1}^N m_i x_i}{\sum_{i=1}^N m_i} = \frac{1}{M} (\sum_{i=1}^N m_i x_i)$
  • Podemos estender os resultados anteriores para as outras direções espaciais:
  • $x_{cm} = \frac{1}{M} (\sum_{i=1}^N m_i x_i)$
  • $y_{cm} = \frac{1}{M} (\sum_{i=1}^N m_i y_i)$
  • $z_{cm} = \frac{1}{M} (\sum_{i=1}^N m_i z_i)$
  • Seja, $\vec{r}_{cm} = x_{cm} \hat{i} + y_{cm} \hat{j} + z_{cm} \hat{k}$,
  • podemos afirmar em notação vetorial que $$\vec{r}_{cm} = \frac{1}{M} (\sum_{i=1}^N m_i \vec{r}_i),$$ onde $\vec{r}_i$ indica a posição da massa $m_i$.

2 massas

  • $\vec{r}{cm} = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1+m_2}$
  • O C.M. está localizado mais próximo da maior massa.
  • No caso de 2 massas, podemos ver ainda que o C.M. sempre está sobre a reta que liga as duas massas.
  • Prova: basta mostrar que o vetor do C.M. para a massa $1$ é paralelo ao vetor que liga as massas $1$ e $2$.
  • $\vec{r}_{1} - \vec{r}_{cm} = \vec{r}_1 - \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1+m_2} = -\frac{m_2}{m_1+m_2} (\vec{r}_2-\vec{r}_1)$.
  • Ou seja, $\vec{r}_{1} - \vec{r}_{cm}$ é paralelo a $(\vec{r}_2-\vec{r}_1)$.

Corpo massivo

  • Objetos do quotidiano possuem sua massa distribuida no espaço. i.e., não são pontuais.
  • Como obter o centro de massa?
  • podemos "fatiar" o objeto em pequenos pedaços de massa $\Delta m$, tal que $$ \vec{r}_{cm} = \frac{\sum_{i=1}^N \vec{r}_i dm}{\sum_{i=1}^N dm} \stackrel{\left(\Delta m\rightarrow0\right)}{\longrightarrow} \vec{r}_{cm} = \frac{\int \vec{r} dm}{\int dm} = \frac{1}{M} \int \vec{r} dm $$
  • Em geral, é mais usual considerar a densidade local $\rho$ $$ \rho = \frac{\Delta m}{\Delta V} \rightarrow \frac{dm}{dV}, $$onde $dV$ é um volume infinitesimal. Daí, $dm = \rho dV$.
  • Para um corpo homogêneo, $\rho = $cte. Substituindo na equação para o CM, $$\vec{r}_{cm} = \frac{\int \vec{r} \rho dV}{\int \rho dV} = \frac{\rho \int \vec{r} dV}{\rho \int dV} = \frac{1}{V} \int \vec{r} dV $$

Exemplo

Calcular a posição do centro de massa ao longo da barra para uma barra sólida de comprimento $L$ e área transversal $A$.

  • $dV = A dx$, e $V = \int_0^L A dx = A L$
  • Então, $x_cm = \frac{1}{AL} \int_0^L x A dx = \frac{1}{L} \left.\frac{x^2}{2}\right|_{x=0}^L = \frac{L}{2}$

2ª Lei de Newton para sistemas de muitas partículas

  • Por que o C.M. é importante?
  • Note que $\vec{r}_{cm} = \frac{1}{M} (\sum_{i=1}^N m_i \vec{r}_i)$, ou $$M \vec{r}_{cm} = \sum_{i=1}^N m_i \vec{r}_i$$
  • Derivando em relação ao tempo, $$M \vec{v}_{cm} = \sum_{i=1}^N m_i \vec{v}_i$$.
  • Podemos ver também que $$M \vec{a}_{cm} = \sum_{i=1}^N m_i \vec{a}_i = \sum_{i=1}^N \vec{F}_{R,i},$$ onde $\vec{F}_{R,i}$ é a força resultante que atua sobre a partícula $i$.
  • Note que forças entre partículas formam pares ação-reação, de forma que ao somar as forças que atuam sobre todas as partículas podemos desconsiderar as forças internas
  • Então, $M \vec{a}_{cm} = \sum \text{(Forças externas que atuam sobre as partículas)}$.
  • O C.M. se comporta como uma partícula pontual de massa $M$ sob ação de todas as forças externas, e é independente dos detalhes da distribuição de partículas
  • Ex.: em fogos de artifício, a trajetória do C.M. não muda com a explosão do artefato.

Momento linear

  • Ao falar da 2ª Lei de Newton, haviamos falado da "quantidade de movimento" $$\vec{p} = m \vec{v}. $$ De agora em diante, nos referiremos a $\vec{p}$ como momento linear.
  • $\vec{p}$ está relacionado com a "dificuldade" em se modificar o movimento de um objeto.
  • 2ª Lei de Newton: $$\frac{d\vec{p}}{dt} = \vec{F}_{R}$$
  • Também podemos reescrever a energia cinética em termos de $\vec{p}$: $K = \frac{1}{2}mv^2=\frac{p^2}{2m}$
  • Para um sistema de partículas, $$ \vec{P} = M \vec{v}_{cm} $$ é o momento linear total do sistema
  • Notar que, se a massa total não varia, $$ \frac{d\vec{P}}{dt} = M\frac{d\vec{v}_{cm}}{dt} = M\vec{a}_{cm} = \vec{F}_{R} $$
  • Ou seja, para um sistema de partículas, a força resultante $\vec{F}_R$ varia o momento linear total do sistema

Colisão e impulso

  • Como representar o que acontece durante a colisão entre dois corpos?
  • Seja $\vec{F}$ a força devido à colisão,
  • $\frac{d\vec{p}}{dt} = \vec{F}$, e integrando em relação a $t$ em ambos os lados, $$\int_{t_0}^{t_1}\frac{d\vec{p}}{dt} dt = \Delta \vec{p} = \int_{t_0}^{t_1}\vec{F} dt = \vec{J}$$
  • $\Delta \vec{p}$: variação do momento linear
  • $\vec{J} = \int_{t_0}^{t_1}\vec{F} dt$: Impulso devido a $\vec{F}$
  • Daí, podemos afirmar que $$ \Delta \vec{p} = \vec{J} $$
  • Em geral, $\vec{F}$ é uma função complicada do tempo. Daí, costuma-se expressar o impulso em termos da força média realizada durante o intervalo de tempo $\Delta t = t_1-t_0$, $$ \vec{J} = \vec{F}_{med} \Delta t $$
from scipy.interpolate import spline

prepend = [[0,0], [2,0]]
postpend = [[6,0], [8,0]]

def apply_pre_post(x, y):
    new_values = len(prepend)+len(postpend)
    buff_x = zeros(x.shape[0]+new_values)
    buff_y = zeros(y.shape[0]+new_values)
    for i, elem in enumerate(prepend):
        buff_x[i] = elem[0]
        buff_y[i] = elem[1]
    ishift = len(prepend)
    buff_x[ishift:(ishift+x.shape[0])] = x
    buff_y[ishift:(ishift+x.shape[0])] = y
    ishift = len(prepend)+x.shape[0]
    for i, elem in enumerate(postpend):
        buff_x[ishift+i] = elem[0]
        buff_y[ishift+i] = elem[1]
    return buff_x, buff_y

x = array([2,3,4,5,6])
y = array([0,6,2,1,0])
xspline = linspace(x[0],x[-1], 100)
yspline = spline(x, y, xspline)
x_full, y_full = apply_pre_post(xspline, yspline)

avg_impulse = sum(yspline)*(xspline[1]-xspline[0])/(x[-1]-x[0])

x, y = apply_pre_post(array([2,6]), avg_impulse*array([1,1]))

subplot(121)
plot(x_full, y_full)
fill_between(x_full, y_full, alpha=0.3)

ylim(-0.2,6.4)
xlabel('t (s)')
ylabel('F (N)')
xticks([2,6], [r'$t_0$', r'$t_1$'])
yticks([avg_impulse, yspline.max()], [r'$F_{med}$', r'$F_{max}$']);

subplot(122)
plot(x, y)
fill_between(x, y, alpha=0.3)

ylim(-0.2,6.4)
xlabel('t (s)')
ylabel('F (N)')
xticks([2,6], [r'$t_0$', r'$t_1$'])
yticks([avg_impulse, yspline.max()], [r'$F_{med}$', r'$F_{max}$']);
tight_layout()

Pergunta

Um paraquedista, cujo paraquedas não abriu, cai em um monte de neve e sofre ferimentos leves. Se caísse em um terreno sem neve, o tempo necessário para parar teria sido 10 vezes menor e a colisão teria sido fatal. Devido à presença da neve, a variação do momento do paraquedista:

  1. Aumenta
  2. Diminui
  3. Permanece igual
  4. Não é possível afirmar nada

Pergunta

Um paraquedista, cujo paraquedas não abriu, cai em um monte de neve e sofre ferimentos leves. Se caísse em um terreno sem neve, o tempo necessário para parar teria sido 10 vezes menor e a colisão teria sido fatal. Devido à presença da neve, o impulso experimentado pelo paraquedista:

  1. Aumenta
  2. Diminui
  3. Permanece igual
  4. Não é possível afirmar nada

Pergunta

Um paraquedista, cujo paraquedas não abriu, cai em um monte de neve e sofre ferimentos leves. Se caísse em um terreno sem neve, o tempo necessário para parar teria sido 10 vezes menor e a colisão teria sido fatal. Devido à presença da neve, força média experimentada pelo paraquedista:

  1. Aumenta
  2. Diminui
  3. Permanece igual
  4. Não é possível afirmar nada

Conservação do momento linear

  • $\frac{d\vec{P}}{dt} = \vec{F}_{R, externas}$
  • Se o sistema é isolado e não há forças externas, $\vec{F}_{R, externas} = 0$
  • Neste caso, $\frac{d\vec{P}}{dt} = 0$, e $$\vec{P}=\vec{\text{cte}}$$
  • Na ausência de forças externas, o momento linear total do sistema é conservado (lei de conservação do momento linear)
  • Note que em geral existem forças internas não nulas! Ex.: Uma caixa sobre um plano horizontal não possui força resultante, mas existem forças internas não nulas que unem as moléculas que compõem a caixa.
  • Note ainda que $\vec{P}=m\vec{v}_{cm}=\vec{\text{cte}}$ implica que o C.M. descreve um movimento retilíneo uniforme

Exemplo - Livro texto

A Figura abaixo mostra um rebocador espacial e uma cápsula de carga, de massa total M, viajando ao longo de um eixo x no espaço sideral com uma velocidade inicial $\vec{v}_i$ de módulo 2100 km/h em relação ao Sol. Com uma pequena explosão, o rebocador ejeta a cápsula de carga, de massa $0,20M$. Depois disso, o rebocador passa a viajar 500 km/h mais depressa que a cápsula ao longo do eixo $x$, ou seja, a velocidade relativa $v_{rel}$ entre a cápsula e o cargueiro é de 500 km/h. Qual é, nesse instante, a velocidade $v_{RS}$ do rebocador em relação ao Sol?

fig

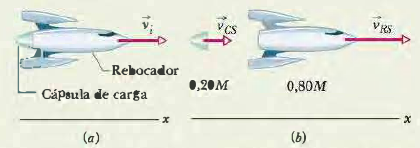
R.: $v_{RS} = 2200$ km/h