Até aqui vimos...¶
- Cinemática de 1 partícula $\rightarrow$ Leis de Newton.
- Trabalho e energia. Até aqui, 1 corpo apenas.
- 2 ou mais corpos: conservação de momento linear total $\rightarrow$ colisões. Centro de massa de um objeto extenso.
- O que vimos até agora permite compreender um objeto que translada no espaço.
- E se o objeto gira? E se temos um sistema de partículas que gira?
Definições importantes¶
- Corpo rígido: todas as suas dimensões são fixas durante o movimento. Sua forma não muda (ex.: sólido).
- Consideraremos a rotação de um corpo rígido em torno de um eixo fixo.
- Eixo fixo: a posição e orientação do eixo são constantes. Exclui rolamento por exemplo (+ adiante!).
- Eixo de rotação:
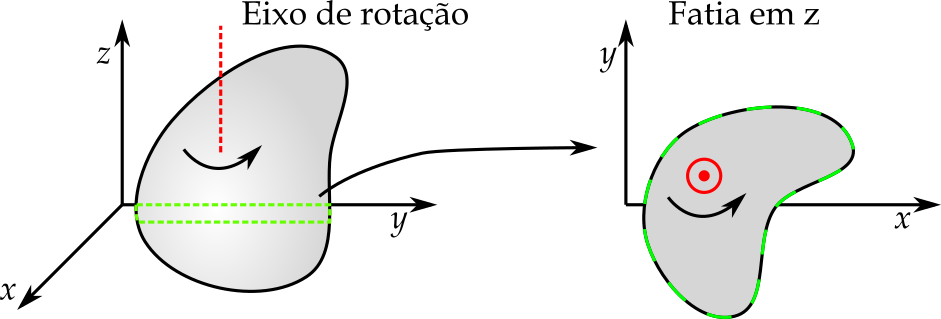
Reta de referência e posição angular¶
- Determina o ângulo '$0$'. Ex.: uma corte transversal do objeto em rotação
- Eixo 'x' é a referência para a tomada de ângulo.
- Como representar $\theta$ termos de $r$ e do comprimento de arco $s$?
- $\theta = \frac{s}{r} \rightarrow \theta$ é a posição angular. Pode assumir qualquer valor real.
- $\theta$ é dado sempre em radianos!
- Como fica a cinemática dos movimentos de rotação?
Deslocamento angular¶
- $\Delta\theta = \theta_2 - \theta_1$
- O deslocamento angular é o mesmo para todas as partes do corpo.
- $\Delta\theta>0$ para rotação no sentido anti-horário.
- $\Delta\theta<0$ para rotação no sentido horário.
- "Relógios são negativos".
Velocidade angular¶
- Quão rápido ocorre o deslocamento angular?
- Velocidade angular média: $\omega_{med} = \frac{\theta_2-\theta_1}{t_2-t_1} = \frac{\Delta\theta}{\Delta t}$.
- Velocidade angular instantânea: $\omega = \frac{d\theta}{d t}$.
- Vale para todas as partículas que compõem o corpo rígido
- Aceleração angular instantânea: $\alpha = \frac{d\omega}{d t} = \frac{d^2\theta}{d t^2}$.
Rotações no espaço¶
- $\omega = \frac{d\theta}{d t}$ é um escalar.
- Para translações, temos que em em 3D podemos representar as grandezas posição, velocidade e aceleração em termos de vetores ($\vec{r}, \vec{v}, \vec{a}$...)
- Podemos girar em torno de 3 eixos ($x$, $y$ e $z$)... É possível representar as grandezas de rotação por vetores?
- R.: Sim, porém com ressalvas. Além disto, precisaremos de um tipo diferente de vetor...
Rotação em torno de um eixo fixo¶
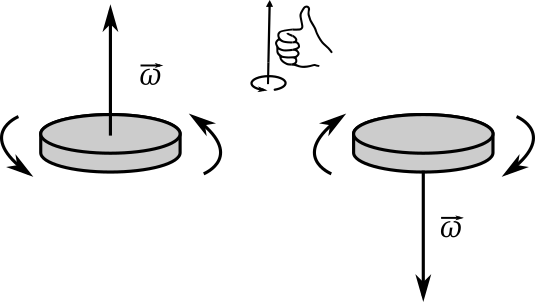
- $\Delta \theta$, $\omega$ e $\alpha$ podem ser representados como escalares.
- Para definir um vetor associado a $\omega$, podemos usar a regra da mão direita para definir a direção e o sentido do vetor.
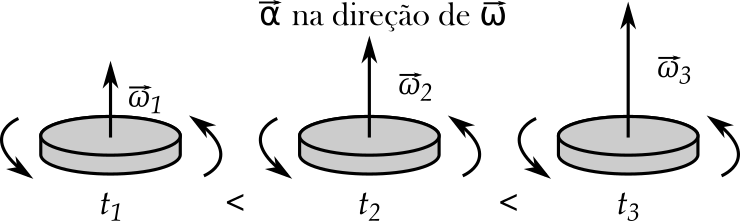
Aceleração angular vetorial¶
- $\vec{\alpha}=\frac{d\vec{\omega}}{dt}$, e
- E $\Delta \vec{\theta}$? Pode ser definido?
- Deslocamentos angulares finitos não são vetores! (Podem ser representadas pelas denominadas matrizes de Euler)
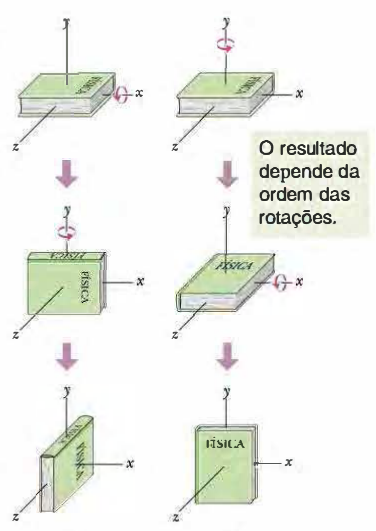
Exemplo: rotações em torno dos eixos $x$ e $y$¶
- Modificando a ordem das rotações, obtém-se uma situação ("estado") final distinto.
- Apenas deslocamentos angulares infinitesimais satisfazem as regras de comutatividade: $R_x(\theta_1).R_y(\theta_2)\approx R_y(\theta_2).R_x(\theta_1)$
Alguns casos especiais¶
- Em cinemática, discutimos o MRU e o MRUV, onde $v=$cte e $a=$cte, respectivamente.
- Quais seriam os análogos para rotação?
- Descrevendo a rotação em termos de escalares, podemos montar um dicionário que relaciona translação e rotação
- $x\rightarrow\theta$, $v\rightarrow\omega$ e $a\rightarrow\alpha$
- Ex.: análogo do MRUV:
- $v = v_0 + a t \rightarrow \omega = \omega_0 + \alpha t$
- $x = x_0 + v_0t + at^2/2 \rightarrow \theta = \theta_0 + \omega_0 t + \alpha t^2/2$
Relação entre variáveis lineares e angulares¶
- $\theta=\frac{s}{r}$, ou $s = \theta r$.
- Para um corpo rígido preso a um eixo fixo, $r=$cte
- Como calcular o módulo da velocidade?
- $v = \frac{ds}{dt}=\frac{d\theta}{dt} r = \omega r$
- Período de revolução: $v = \frac{2 \pi r}{T}$, ou $T = \frac{2\pi r}{\omega r} = \frac{2\pi}{\omega}$ ($\omega$ em Rad/s!)
Aceleração¶
- No Movimento Circular Uniforme, ($\omega=$cte, $|\vec{v}|=v=$cte), $\vec{a}$ é na direção radial.
- Lembrando, $a_{cpt} = \frac{v^2}{r} = \omega^2 r \rightarrow$ aceleração centrípeta.
- Se $v=\omega r$ varia e $r=$cte, $\frac{dv}{dt}=?$
- $\frac{dv}{dt} = \frac{d(\omega r)}{dt} = \frac{d\omega}{dt} r = \alpha r \equiv$ aceleração tangencial $=a_t$.
- No caso geral, temos $$ \vec{a} = \vec{a}_{cpt} + \vec{a}_{t} $$
Demonstração de $\vec{a} = \vec{a}_{cpt} + \vec{a}_{t}$¶
- Seja $\vec{r} = r [\cos\theta(t) \hat\imath + \sin\theta(t)\hat\jmath]$, $\vec{v}=\frac{d\vec{r}}{dt}$
- $\vec{v}=r\frac{d[\cos\theta(t) \hat\imath + \sin\theta(t)\hat\jmath]}{dt} = r[\frac{d\cos\theta(t)}{dt} \hat\imath + \frac{\sin\theta(t)}{dt}\hat\jmath]$
- $\frac{d\cos\theta(t)}{dt} = \frac{d\cos\theta}{d\theta}\frac{d\theta}{dt} = (-\sin\theta)\omega$, e analogamente $\frac{d\sin\theta(t)}{dt} = (\cos\theta)\omega$.
- Então, $\vec{v} = \omega(t) r[-\sin\theta(t) \hat\imath + \cos\theta(t)\hat\jmath]$.
Demonstração de $\vec{a} = \vec{a}_{cpt} + \vec{a}_{t}$¶
- Finalmente para a aceleração, temos $\vec{a} = \frac{d\vec{v}}{dt}$, ou
- $\vec{a} = \frac{d}{dt} \{\omega(t) r[-\sin\theta(t) \hat\imath + \cos\theta(t)\hat\jmath]\}$.
- $\vec{a} = \{\frac{d\omega(t)}{dt} r[-\sin\theta(t) \hat\imath + \cos\theta(t)\hat\jmath]\} + \omega(t) r[-\frac{\sin\theta(t)}{dt} \hat\imath + \frac{\cos\theta(t)}{dt}\hat\jmath]$.
- $\vec{a} = \alpha r[-\sin\theta(t) \hat\imath + \cos\theta(t)\hat\jmath] - \omega^2(t) r[\cos\theta(t) \hat\imath + \sin\theta(t)\hat\jmath]$.
- $\vec{a} = \frac{\alpha}{\omega} \vec{v} - \omega^2 \vec{r}$.
- $\vec{a}_t = \frac{\alpha}{\omega} \vec{v}$: aceleração tangencial
- $\vec{a}_{cpt} = - \omega^2 \vec{r}$: aceleração centrípeta
Energia cinética de rotação¶
- Se as partículas que compõem o objeto estão em movimento, estas possuem energia cinética.
- Qual é a energia cinética de um corpo em rotação?
- Consideremos um conjunto de partículas de massas $m_1,m_2, m_3,\dots$ e velocidades $\vec{v}_1,\vec{v}_2,\vec{v}_3,\dots$.
- Energia cinética total: $K = \frac{1}{2} m_1v_1^2 + \frac{1}{2} m_2v_2^2 + \frac{1}{2} m_3v_3^2 + \dots = \sum_{i=1}^N \frac{1}{2} m_iv_i^2$
- Para um corpo rígido, $v_i = \omega r_i$, onde $r_i$ é a distância entre o eixo de rotação e a partícula
Energia cinética de rotação¶
- Energia cinética total: $K = \sum_{i=1}^N \frac{1}{2} m_i(\omega r_i)^2$
- $K=\frac{1}{2} \left[\sum_{i=1}^N m_i r_i^2\right] \omega^2 = \frac{1}{2} I \omega^2$ (Rotação)
- Análogo a $K=\frac{1}{2} m v^2$ (Translação)
- Momento de inércia em relação ao eixo de rotação: $$I = \sum_{i=1}^N m_i r_i^2$$
- Importante! $I$ só faz sentido se sabemos qual o eixo de rotação!
- Unidade de $I$ no SI: kg.m$^2$
Momento de inércia¶
- $I = \sum_{i=1}^N m_i r_i^2$
- Similarmente ao que fizemos para cálculo do centro de massa, podemos calcular $I$ para uma distribuição contínua de massa fazendo $m\rightarrow dm$, e $$I = \int r^2 dm$$
- Fisicamente, o que $I$ representa?
- $K=\frac{1}{2} I \omega^2$ é análogo a $K=\frac{1}{2} m v^2$
- $\omega$ e $v$ são velocidades, enquanto $I$ e $m$ estão relacionado com a inércia.
- Importante! $I$ depende não apenas da massa, mas também da sua distribuição no espaço!
Exemplo¶
- $I = \sum_{i=1}^N m_i r_i^2 \rightarrow \int r^2 dm$
- Quem é maior, $I_1$ ou $I_2$?
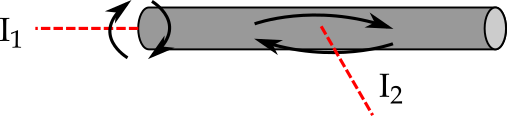
- $I_2>I_1$, pois a massa está distribuida mais distante do eixo de rotação. ($r$ é tipicamente maior)
Cálculo do momento de inércia¶
- $I = \sum_{i=1}^N m_i r_i^2 \rightarrow \int r^2 dm$
- Ex.: anel fino de massa $M$ em torno do eixo central
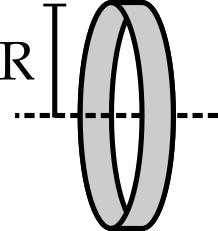
- $I = \int r^2 dm$. Mas, $r=R$ para todos os elementos de massa!
- $I = R^2 \int dm = MR^2$
Cálculo do momento de inércia¶
- $I = \sum_{i=1}^N m_i r_i^2 \rightarrow \int r^2 dm$
- Ex.: barra fina em torno de um eixo central perpendicular
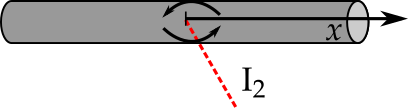
- $I=\int x^2 dm = \int_{-L/2}^{L/2} x^2 \frac{M}{L} dx = \frac{M}{L} \left[\frac{(L/2)^3}{3}-\frac{(-L/2)^3}{3}\right]$
- $I = \frac{ML^2}{12}$
Cálculo do momento de inércia¶
- Ex.: Disco (ou barra) em torno do eixo central.
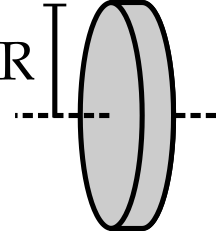
- $I=\int r^2 dm$. Quem é $dm$?
- Imaginemos uma pequena casca cilíndrica, tal que corresponde à fração de massa da casca cilíndrica $dm = M \frac{2 \pi r dr L}{\pi R^2 L}$
- $I=\int_0^R r^2 \frac{2r dr}{R^2} = \frac{2}{R^2} \left(\frac{R^4}{4} - \frac{0^4}{4}\right)$
- $I=\frac{MR^2}{2}$
- Para outras geometrias, consultar o livro!
Teorema dos eixos paralelos¶
- Caso o momento de inércia seja conhecido em um eixo que passe pelo centro de massa (C.M.), podemos encontrar o momento de inércia em qualquer eixo paralelo ao original. $$ I = I_{cm} + Mh^2, $$ onde $h$ representa a distância entre o C.M. e o novo eixo.
- Demonstração:
- $I=\int (\text{distância})^2 dm$. Sejam $\vec{r} = x\hat\imath + y \hat\jmath$ e $\vec{s} = a\hat\imath + b \hat\jmath$
- $I=\int \left[(x-a)^2+(y-b)^2\right]dm$
- $=\int \left[(x^2-2ax+a^2)+(y^2-2yb+b^2)\right]dm$
- $=\int \left[x^2+y^2\right]dm -\int 2\left[ax + by\right]dm + \int \left[a^2+b^2\right]dm$
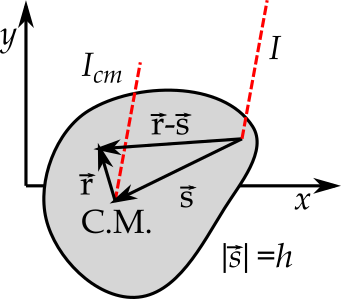
Teorema dos eixos paralelos (demonstração)¶
- $\vec{r} = x\hat\imath + y \hat\jmath$ e $\vec{s} = a\hat\imath + b \hat\jmath$
- $I=\int \left[x^2+y^2\right]dm -2\int \left[ax + by\right]dm + \int \left[a^2+b^2\right]dm$
- $\int \left[x^2+y^2\right]dm = I_{cm}$
- $\int \left[ax + by\right]dm = 0$ (Posição do C.M. em relação ao próprio C.M.)
- $a^2+b^2 = h^2$
- $I = I_{cm} + M h^2$

Exercício¶
Ordene crescentemente os momentos de inércia $I_j$ considerando os eixos a seguir:
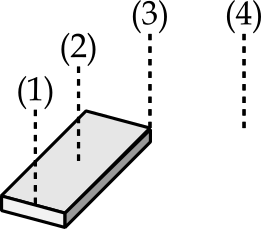
- $I_2\text{<}I_1\text{<}I_3\text{<}I_4$
Exercício¶
Calcular o momento de inércia $I$ para os sistemas de 2 partículas abaixo
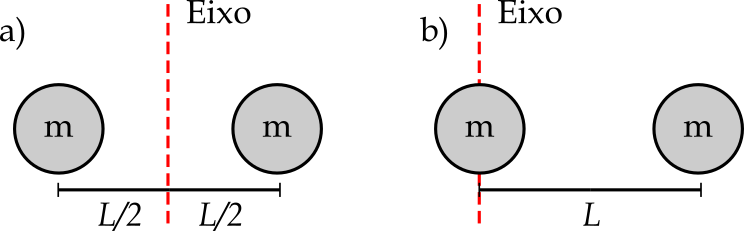
- a) $I = m\left(-\frac{L}{2}\right)^2+m\left(\frac{L}{2}\right)^2 = \frac{mL^2}{2}$
- b) Usando o T.E.P., $I = I_{cm} + 2m \left(\frac{L}{2}\right)^2 = mL^2$
Torque¶
- Por que a maçaneta da porta nunca fica perto da dobradiça?
- O "resultado" da força aplicada depende do ponto de aplicação em relação ao eixo de rotação!
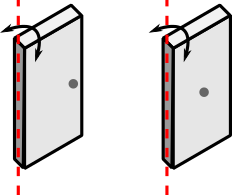
Rotação devido à aplicação de uma força¶
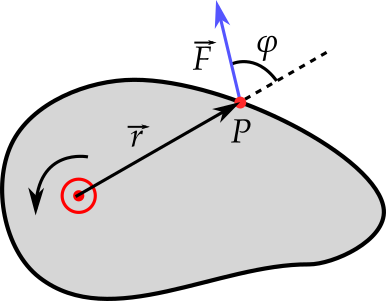
- Consideremos uma força $\vec{F}$ no plano de rotação
- Trabalho realizado por $\vec{F}$: $\Delta W = F \cdot \Delta x$
- Buscamos um análogo para rotações, ou algo do tipo $\Delta W = \tau \Delta\theta$
- Qual o trabalho realizado por $\vec{F}$?
- $F_t = F \sin\phi$ realiza um deslocamento $s = r\Delta\theta$
Rotação devido à aplicação de uma força¶
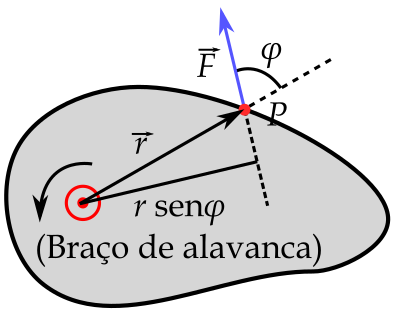
- $\Delta W = \tau \Delta\theta$
- $F_\perp = F \sin\phi$, e $s = r\Delta\theta$
- $\Delta W =$ (Força).(Deslocamento)
- $\Delta W = F \sin\phi\, r\Delta\theta$
- Então, $\tau=F \sin\phi\, r = \left|\vec{r}\times\vec{F}\right|$
- Vetorialmente, $$\vec{\tau}=\vec{r}\times\vec{F}$$
Segunda lei de Newton para rotações¶
- Qual a relação entre o torque e a aceleração angular? (à là $\vec{F}=m\vec{a}$)
- $\tau$ está associado à aceleração tangencial:
- $\tau=r\; F_t = r \; ma_t = r \; m(\alpha r) $
- $\tau=mr^2 \alpha = I \alpha$ $$\tau = I \alpha$$
- Vetorialmente, temos também que $\vec{\tau} = I \vec{\alpha}$
Pergunta¶
Sabendo que $\tau = r\; F_t = I \alpha$, e pensando apenas em diminuir o esforço em abrir uma dada porta para uma dada força aplicada, onde deveria ficar o eixo de rotação da porta, e qual seria a posição ideal para a maçaneta?
R.: O eixo deveria passar pelo centro de massa para diminuir o momento de inércia $I$, enquanto que a maçaneta deve estar o mais distante possível do eixo de rotação. Por que as portas não são feitas assim?
Exercício¶
Considere que um bloco de massa $m=1,2$ kg está preso por uma corda ideal a um disco de massa $M=2,4$ kg e raio $R=20$ cm. Determine a aceleração linear $a$ do bloco, a aceleração angular $\alpha$ do disco e a tração $T$ sobre a corda. Considere ainda que a corda não desliza e o sistema não possui atrito.
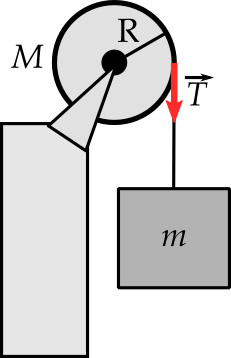
R.: $a = -\frac{2m}{2m+M} g \approx -5$ m/s$^2$, $\alpha = \frac{a}{R} = -25$ rad/s$^2$, $T=-\frac{1}{2}Ma = 6,0$ N
Trabalho e energia cinética de rotação¶
- Vimos anteriormente que para movimentos ao longo de uma direção espacial,
- $W = \int_{x_0}^{x_1} F(x) dx$ (Força variável)
- $W_R = \int_{x_0}^{x_1} F_R(x) dx = \Delta K$ (Teo. Trabalho e Energia Cinética)
- $P = \frac{dW}{dt} = F.v$
- E para movimentos de rotação?
Trabalho e energia cinética de rotação¶
- Vejamos qual é o torque realizado por uma força $\vec{F}$ quando um corpo sofre um deslocamento angular entre $\theta_0$ e $\theta_1$.
- $W = \int_{\vec{r}_0}^{\vec{r}_1} \vec{F}(\vec{r}) d\vec{r} = \int_{\vec{r}_0}^{\vec{r}_1} \vec{F}(\vec{r}) \frac{d\vec{r}}{d\theta} d\theta$
- Note que se $\theta_1,\theta_0\approx0$, então $\Delta \vec{r} = \vec{r}_1-\vec{r}_0 = r\left[(\cos\theta_1-\cos\theta_0)\hat\imath + (\sin\theta_1-\sin\theta_0)\hat\jmath\right] \approx r(\theta_1-\theta_0)\hat\jmath = r\Delta\theta\hat\jmath$
- Então $W = \int_{\theta_0}^{\theta_1} r F_t d\theta$ $$W = \int_{\theta_0}^{\theta_1} \tau d\theta.$$
- Note ainda que se o torque é constante, $$ W = \tau \Delta \theta$$
Energia cinética de rotação e potência¶
- $W = \Delta K = \frac{1}{2} m v_f^2 - \frac{1}{2} m v_i^2$
- Usando a analogia $m\rightarrow I$, $v\rightarrow\omega$,
- $W = \Delta K = \frac{1}{2} I \omega_f^2 - \frac{1}{2} I \omega_i^2$ (Teo. Trabalho e Energia Cinética para sistemas sob rotação).
- Potência: $P = \frac{dW}{dt} = \frac{Fdx}{dt} = \frac{\tau d\theta}{dt}$ $$P=\tau \omega$$
Alguns problemas¶
Exemplo¶
Considerando o disco de massa $M=2,4$ kg e raio $R=20$ cm do exemplo anterior, com uma velocidade angular inicial $\omega_0=0$ e $\alpha=25$ rad/s$^2$. Qual é a energia cinética de rotação do disco em $t=2$ s?
R.: $K = \frac{M}{4} (R \alpha t)^2$ = 60 J
Problema 10.63 (9a Ed.): Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremidade de apoio não escorrega. (Sugestão: considere a régua uma barra fina e use a lei de conservação da energia.)
Dado.: Para uma barra fina, $I_{cm} = \frac{ML^2}{12}$.
$v = \sqrt{3gL} \approx 5,4$ m/s
Problema 10.66 (9a Ed.) Uma casca esférica homogênea de massa $M = 4,5$ kg e raio $R = 8,5$ cm pode girar em torno de um eixo vertical sem atrito, conforme a figura. Uma corda de massa desprezível está enrolada no equador da casca, passa por uma polia de momento de inércia $I = 3,0 \times 10^{-3}$ kg$\cdot$m$^2$ e raio $r = 5,0$ cm e está presa a um pequeno objeto de massa $m = 0,60$ kg. Não há atrito no eixo da polia e a corda não escorrega na casca nem na polia. Qual é a velocidade do objeto depois de cair $82$ cm após ter sido liberado a partir do repouso? Use considerações de energia.
Dado: $I_{cm, Esfera} = \frac{2MR^2}{3}$
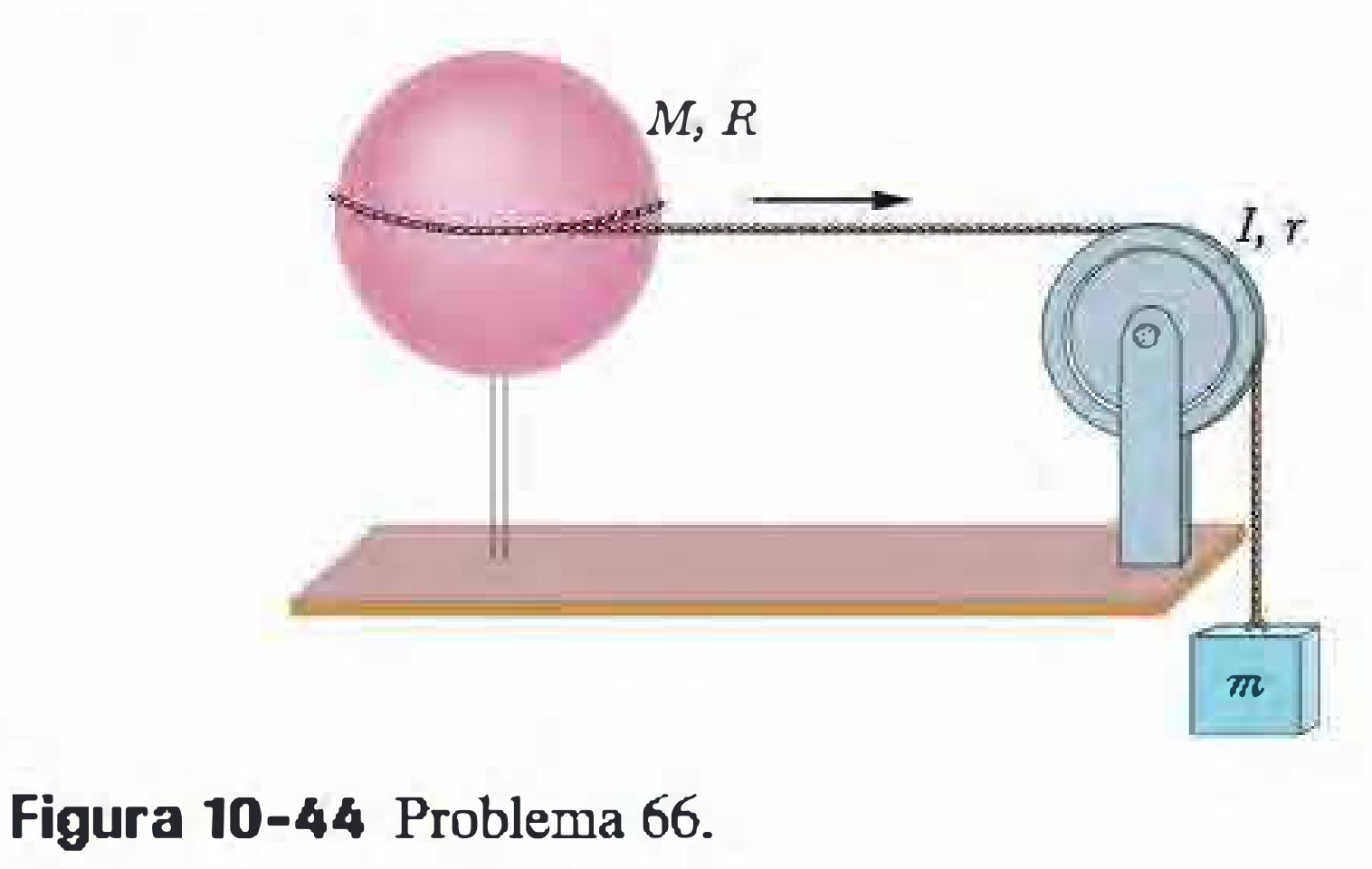
R.: $v_m = \sqrt{\frac{m g h}{\frac{M}{3} + \frac{I}{2r^2} + \frac{m}{2}}} = 1,42$ m/s


