Cinemática rotacional¶
- Posição Angular: $\theta = \frac{s}{r}$, ($s$: arco de círculo, $\theta$ em radianos)
- Deslocamento Angular: $\Delta \theta = \theta_2-\theta_1$
- Positivo no sentido anti-horário
- Velocidade Angular: $\omega = \frac{d\theta}{dt}$
- Vetorialmente, $\vec{\omega}$ pode ser encontrado pela regra da mão direita ($\vec{r}\times\vec{v}$)
- Aceleração Angular: $\alpha = \frac{d\omega}{dt}$
- Equações cinemáticas: Similares ao caso de translação, trocando $x$, $v$ e $a$ respectivamente por $\theta$, $\omega$ e $\alpha$.
2016.1 - Questão 1¶
A posição angular de um ponto de uma roda é dada por, $$ \theta(t) = 3 + 12 t^2 - t^4, $$ onde $\theta$ está em radianos e $t$ em segundos. Em $t = 2,0\text{ s}$ a velocidade angular do ponto é igual a $\boxed{\qquad\phantom{\dfrac{x}{y}}}\text{ rad/s}$, enquanto que a aceleração angular é igual a $\boxed{\phantom{\qquad\dfrac{x}{y}}}\text{ rad/s}^2$.
R.: $\omega = 16$ rad/s e $\alpha = -24$ rad/s$^2$
Relação entre variáveis lineares e angulares¶
- $s = \theta r$
- $v = \omega r$
- $\vec{a}$ contém 2 componentes:
- Tangencial: $a_t = \alpha r$
- Radial: $a_r = \frac{v^2}{r}$
- Periodo do movimento: $T = \frac{2\pi r}{v} = \frac{2\pi}{\omega}$
2016.1 - Questão 2¶
Uma roda dentada de raio $r_1$ está acoplada a uma segunda roda dentada de raio $r_2 = \dfrac{r_1}{2}$ por uma correia, como mostra a figura. A roda de raio $r_2$ é fixada coaxialmente a uma roda de raio $R = 0,40$ m, formando um sistema que gira como um único corpo. As rodas podem girar livremente em um plano horizontal em torno de eixos verticais fixos que passam pelos pontos $1$ e $2$. Quando a roda de raio $r_1$ gira com velocidade angular igual a $\omega = 4,0$ rad/s, o módulo da velocidade do ponto $C$ é igual a $\boxed{\phantom{\qquad\dfrac{x}{y}}}\text{ m/s}$.
R.: $v=3,2$ m/s
Energia cinética de rotação e momento de inércia¶
- Energia cinética de rotação: $K_R = \frac{I\omega^2}{2}$
- O corpo pode possuir uma energia cinética de translação também ($K_T = \frac{mv^2}{2}$)!
- Energia cinética total: $K = \frac{mv^2}{2} + \frac{I\omega^2}{2}$.
- Momento de inércia $I$: "Dificuldade" em variar o movimento rotacional
- Partículas: $I = \sum_i m_i r_i^2$.
- Corpo contínuo: $I = \int r^2 dm$
- Teorema dos eixos paralelos
- $I = I_{CM} + M h^2$: Menor momento de inércia é o que passa pelo centro de massa ($I_{CM}$)
- $M$: massa total do corpo. $h$: Distância entre C.M. e o eixo de rotação considerado.
2016.2 - Questão 2¶
Um corpo rígido é formado por três partículas de massas $m_1 = m$, $m_2 = 3m$ e $m_3 = 5m$ conectados por hastes de comprimento $\ell$ cada, como mostra a figura 2. As massas das hastes são desprezíveis. Qual é o momento de inércia do corpo em relação ao eixo de rotação representado pela reta tracejada?
(a) $I = 21 m\ell^2$ (b) $I = 9 m\ell^2$ (c) $I = 17 m\ell^2$ (d) $I = 23 m\ell^2$ (e) $I = 13 m\ell^2$ (f) $I = 7 m\ell^2$
R.: (d)
Torque e energia¶
- $\vec{\tau} = \vec{r}\times\vec{F}$
- Em módulo, $\tau = r F \text{sen}\phi$, onde $\phi$ é o ângulo relativo entre $\vec{r}$ e $\vec{F}$.
- $\vec{\tau}$ tem a mesma direção de $\omega$ e $\alpha$. $\tau$ é positivo se o torque produz uma aceleração angular no sentido anti-horário, e negativo no caso oposto.
- 2ª Lei para rotações: Torque resultante $\tau_{res} = I \alpha$.
- Trabalho: $W = \int_{\theta_i}^{\theta_f} \tau d\theta$
- Potência: $P = \frac{dW}{dt} = \tau \omega$
- Teorema do trabalho-energia cinética: $W = \Delta K = \frac{I\omega_f^2}{2} - \frac{I\omega_i^2}{2}$
2016.1 - Questão 3¶
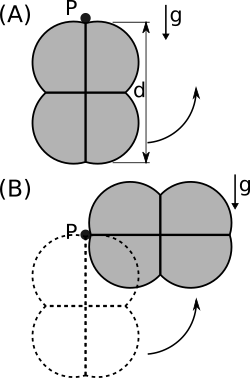
Um corpo rígido, de comprimento $d$ e massa $m$, pode girar livremente em torno de um eixo perpendicular ao plano do papel que passa pelo ponto $P$ com momento de inércia $I_P$. O centro de massa do corpo se situa a uma distância $d/2$ do ponto $P$. Na posição mostrada na Fig. (A) o corpo possui velocidade angular suficiente para atingir a posição mostrada na Fig. (B) com velocidade angular zero. Considere as afirmações abaixo:
(I) O módulo do torque da força gravitacional sobre o corpo em relação ao ponto P na situação mostrada na Fig. (B) é $m g d$.
(II) O módulo do momento angular do corpo em relação ao ponto $P$ quando na posição mostrada na Fig. (A) é igual a $\sqrt{m g d I_P}$.
(III) O módulo do torque da força gravitacional sobre o corpo em relação ao ponto P na situação mostrada na Fig. (B) é $m g d/2$.
(IV) O módulo da velocidade angular do corpo na posição mostrada na Fig. (A) é igual a $\sqrt{2 m g d/I_P}$.
Qual alternativa lista todos os itens corretos?
(a) I, (b) I e II, (c) II, (d) I e IV, (e) II e IV, (f) II e III,(g) III, (h) IV
R.: (f)
2016.2 - Questão 4¶
Um sistema é constituído por uma roldana e um bloco de massa $m$ conectados por um fio inextensível e de massa deprezível, como mostra a figura. A roldana, de raio $r$, pode girar livremente em torno de um eixo fixo perpendicular à página e que passa pelo seu centro de massa, com momento de inércia $I$ em relação a este eixo. O fio não desliza sobre a roldana. Sabe-se que inicialmente o sistema está em repouso [figura 4(I)] e que, após ter descido uma altura $h$ [figura 4(II)], $v$ é o módulo da velocidade do bloco e $\omega$ é o módulo da velocidade angular da roldana. Marque a alternativa correta:
(a) $v = \sqrt{2 g h}$, $\omega r = v$, (b) $v < \sqrt{2 g h}$, $\omega r < v$, (c) $v = \sqrt{2 g h}$, $\omega r > v$, (d) $v > \sqrt{2 g h}$, $\omega r = 0$, (e) $v < \sqrt{2 g h}$, $\omega r = v$, (f) $v > \sqrt{2 g h}$, $\omega r = v$
R.: (e)
Rolamento suave¶
- $v_{CM} = \omega R$
- $v{CM}$: Vel. do centro de massa da roda
- $R$: Raio da roda
- $a_{CM} = \alpha R$
- Energia cinética total: $K=\frac{1}{2} I_{CM} \omega^2 + \frac{1}{2} M v_{cm}^2$
- $I_{CM}$: Momento de inércia em torno do centro de massa
- $M$: Massa total do corpo
- Roda descendo um plano de ângulo $\theta$ com a horizontal:
- $a_{CM} = \frac{g \text{sen}\theta}{1+I_{CM}/MR^2}$
- $a_{CM}$ diminui com $I_{CM}$ devido ao rolamento.
2016.2 - Questão 4¶
Uma esfera maciça e um aro circular, com massas $m$ iguais e raios $r$ iguais, são liberados a partir do repouso a uma altura $H$ do ponto $C$ (ver figura ao lado), um de cada vez, rolando sem deslizar sobre uma rampa, cujo trecho final é um arco de circunferência de raio $R > r$. $K_1$ e $K_2$ são as energias cinéticas da esfera maciça e do aro respectivamente, enquanto $\vec N_1$ e $\vec N_2$ denotam as forças normais no ponto mais baixo da trajetória (ponto $C$) que atuam sobre a esfera maciça e sobre o aro respectivamente. É correto afirmar que:
(a) $N_1 > N_2$, $K_1 = K_2$, (b) $N_1 = N_2$, $K_1 > K_2$, (c) $N_1 = N_2$, $K_1 < K_2$, (d) $N_1 < N_2$, $K_1 = K_2$
(e) $N_1 > N_2$, $K_1 > K_2$, (f) $N_1 = N_2$, $K_1 = K_2$, (g) $N_1 > N_2$, $K_1 < K_2$, (h) $N_1 < N_2$, $K_1 < K_2$
R.: (a) (O momento de inércia da esfera é menor que o do aro!)
2016.2 - Questão 7¶
Uma bola de raio $r$, massa $m$ e momento de inércia em relação ao centro de massa $I_{\rm CM} = 2m r^2/5 $, rola suavemente sobre um relevo, conforme mostra a figura. No ponto A o módulo da velocidade de centro de massa da bola é igual a $5,00\text{ m/s}$. Ao passar pelo ponto mais alto da trajetória (ponto B), a bola se encontra na iminência de perder contato com a pista. Considere que a bola se encontra em rolamento sem deslizar durante toda a sua trajetória e que a aceleração gravitacional local tenha módulo $g = 10\text{ m/s}^2$.
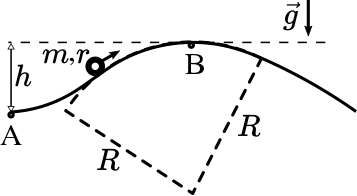
- (a) Determine a energia cinética da bola no ponto A. Considere $m = 1,00\text{ kg}$.
- (b) Calcule o módulo da velocidade do centro de massa da bola ao passar pelo ponto B. O ponto B se encontra a uma altura $h = 0,63\text{ m}$ acima do ponto A.
- (c) Obtenha o raio de curvatura $R$ do trecho da pista onde se encontra o ponto B.
Sugestão: Considere $R \gg r$ e que a força normal é zero na iminência da bola perder contato com a pista.
R.: (a) $K_A = 17,5$ J, (b) $v_{CM,B} = 4,0$ m/s, (c) $R=1,6$ m.
Torque e momento angular¶
- $\vec{\tau} = \vec{r}\times\vec{F}$
- Módulo: $\tau=rF\text{sen}\phi$, onde $\phi$ é o ângulo relativo entre $\vec{r}$ e $\vec{F}$
- Lembrar que a direção do produto vetorial é dada pela regra da mão direita!
- 2ª Lei de Newton para rotações: $$\vec{\tau} = \frac{d\vec{\ell}}{dt}$$
- Momento angular (1 partícula): $\vec{\ell} = \vec{r}\times\vec{p} = m \vec{r}\times\vec{v}$
- Momento angular (N partículas): $\vec{L} = \vec{\ell}_1 + \vec{\ell}_2 + \vec{\ell}_3 + \dots = \sum_{i=1}^N \vec{\ell}_i$
- Seja $\vec{\tau}_{res}$ o torque resultante devido às forças externas, $$\vec{\tau}_{res} = \frac{d\vec{L}}{dt}$$
2016.2 - Questão 5¶
Uma partícula de massa $m=2,0$ kg desliza sem atrito sobre o plano horizontal $xy$ com velocidade constante $\vec{v}= 3,0\,\hat\jmath $ m/s. A partícula cruza o eixo $x$ na posição $\vec{r} = 4,0 \,\hat\imath$ m. O módulo do seu momento angular em relação à origem é $\boxed{\phantom{\qquad\dfrac{x}{y}}}\text{ J}\cdot\text{s}$.
R.: $\ell = 24\text{ J}\cdot\text{s}$
2016.1 - Questão 6¶
Uma barra delgada de massa $m_1=0,30$ kg e comprimento $\ell_1 = 0,60$ m pode girar livremente sobre um eixo fixo perpendicular ao plano do papel que passa por sua extremidade, no ponto $\mathcal{O}$ (vide figura).
- (a) A barra 1 inicialmente tem velocidade angular $\omega_1 = 2,0$ rad/s. Calcule o módulo do momento angular da barra em relação ao ponto $\mathcal{O}$.
- (b) Uma segunda barra delgada, de massa $m_2= 2 m_1$ e comprimento $\ell_2 = 2 \ell_1$, também pode girar livremente sobre o ponto $\mathcal{O}$. Ela está inicialmente parada, quando a primeira barra se choca com ela. As duas então passam a girar grudadas uma na outra, com velocidade angular $\omega_f$. Calcule $\omega_f$.
- (c) Sejam $K_i$ e $K_f$ as energias cinéticas do sistema antes e depois do choque respectivamente. Calcule a razão $K_f/K_i$.
Dado: o momento de inércia de uma barra delgada de comprimento $\ell$ e massa $m$ girando sobre um eixo perpendicular a ela que passa por seu centro de massa é $I_{\rm CM} = m\ell ^2 / 12$.
R.: (a) $L_1 = 0,072$ kg.m^2/s, (b) $\omega_f = \frac{2}{9}$ rad/s, (c) $\frac{K_f}{K_i} = \frac{1}{9}$
Momento angular de um corpo rígido¶
- $L = I \omega$
- Lembrar de $p = m v$
- Sob a ausência de torques externos, o momento angular do sistema é conservado
- $\vec{L}_i = \vec{L}_f =$ cte.
2016.2 - Questão 6¶
Um estudante está sentado em um banco que pode girar livremente sobre um eixo vertical. O estudante, que foi posto para girar com velocidade angular inicial $\omega_i = 6,0$ rad/s, segura dois halteres com os braços abertos. O vetor momento angular $\vec{L}$ do sistema "estudante + halteres + banco" coincide com o eixo de rotação e aponta para cima. O professor pede ao estudante para fechar os braços, o que reduz o momento de inércia do sistema do valor inicial $I_i=4,0$ kg$\cdot$m$^2$ para $I_f=3,0$ kg$\cdot$m$^2$.
- (a) Depois de fechar os braços, a velocidade angular do sistema é $\boxed{\phantom{\qquad\dfrac{x}{y}}}$ rad/s.
- (b) A energia cinética inicial do sistema é igual a $\boxed{\phantom{\qquad\dfrac{x}{y}}}$ J.
- (c) Depois do estudante fechar os braços, a energia cinética do sistema passa a ser $\boxed{\phantom{\qquad\dfrac{x}{y}}}$ J.
R.: (a) 10 rad/s, (b) 90 J, (c) 150 J.
2016.1 - Questão 5¶
Um dispositivo formado por duas polias acopladas, montadas em um eixo horizontal sem atrito, é usado para levantar uma caixa de massa $m = 30$ kg, como esquematizado na figura ao lado. O raio da polia externa é $R=25$ cm e o raio da polia interna é $r=10$ cm. Uma força externa $\vec F$ horizontal é aplicada à corda. O momento de inércia do dispositivo é $\mathcal I=0,30 $ kg m$^2$. Considere $g = 10\text{ m/s}^2$.
- (a) Calcule o módulo da força externa $\vec F$ necessária para elevar ou abaixar a caixa com velocidade constante.
- (b) Supondo que a caixa desce com velocidade constante de módulo $v_0=2,0$ m/s, calcule a energia cinética do conjunto caixa + polias.
Considere agora que, ao invés da força $\vec F$, uma outra força $\vec F'$ passa a atuar sobre a corda, de maneira que a caixa é desacelerada desde a velocidade inicial de módulo $v_0 = 2,0$ m/s até parar, após descer a altura de $h=5,0$ m, com aceleração constante. Nesta situação, calcule:
- (c) a aceleração angular das polias;
- (d) o trabalho realizado por $\vec F'$.
2016.2 - Segunda Chamada - Questão 1¶
Dois blocos, de massas $m_A = 2,0\text{ kg}$ e $m_B = 1,0\text{ kg}$ encontram-se conectados por um fio inextensível e de massa desprezível (ver figura). O bloco B está sobre um plano inclinado, cujos coeficientes de atrito cinético e estático são $\mu_c = 0,3$ e $\mu_e = 0,6$ respectivamente. O fio passa pela borda externa de uma polia de raio $r = 0,50\text{ m}$ e momento de inércia $I= 0,10\text{ kg}\cdot\text{m}^2$. A polia pode girar sem atrito em torno de um eixo perpendicular à página e que passa pelo seu centro. Não há deslizamento entre o fio e a polia. Considere $\text{sen }\theta = 0,8$, $\cos\theta = 0,6$ e o módulo da aceleração gravitacional no local $g = 10 \text{ m/s}^2$.
- (a) Esboce os diagramas de forças que atuam em cada um dos corpos (blocos e polia). Escreva as equações resultantes da segunda lei de Newton para o sistema.
- (b) Calcule o vetor aceleração do bloco A.
- (c) Obtenha os módulos das trações $\vec T_A$ e $\vec T_B$ nos trechos do fio conectados aos blocos A e B respectivamente.
2016.2 - Exame Final - Questão 3¶
Nas figuras ao lado são mostrados dois corpos rígidos que podem girar livremente em torno de um eixo perpendicular à página e que passa pelo ponto $\mathcal{O}$. Na figura (1) temos duas partículas, de massas $m_A = 3m/5$ e $m_B = 2m/5$, conectadas por uma barra de massa desprezível de comprimento $\ell$. Na figura (2) temos um corpo rígido simétrico, de comprimento $\ell$ e massa $m$. Sejam $d_1$ e $d_2$ as distâncias dos centros de massa ao ponto $\mathcal{O}$, enquanto $I_1$ e $I_2 = 0,38 m\ell^2$ são os momentos de inércia em relação ao eixo de rotação, respectivamente, dos corpos em (1) e (2). Assinale a alternativa correta:
(a) $d_{1} > d_{2}$, $I_1 > I_2$ (b) $d_{1} = d_{2}$, $I_1 = I_2$ (c) $d_{1} = d_{2}$, $I_1 < I_2$
(d) $d_{1} > d_{2}$, $I_1 < I_2$ (e) $d_{1} < d_{2}$, $I_1 > I_2$ (f) $d_{1} < d_{2}$, $I_1 < I_2$
R.: (e)
Questões de 2017.1¶
Três massas, $m_1=m$, $m_2 = 2m$ e $m_3=3m$ estão afixadas em uma barra de massa desprezível que gira em torno do eixo $\mathcal{O}$ com velocidade angular $\omega$, conforme a figura.
1$^{\rm a}$ Questão (1,5 pontos): Qual o momento de inércia do conjunto de massas na Figura 1 em relação ao eixo $\mathcal{O}$?
(a) $I = 10 m\ell^2$ (b) $I = 18 m\ell^2$ (c) $I = 26 m\ell^2$ (d) $I = 30 m\ell^2$ (e) $I = 36 m\ell^2$ (f) $I = 40 m\ell^2$
R.: (e)
Questões de 2017.1¶
Três massas, $m_1=m$, $m_2 = 2m$ e $m_3=3m$ estão afixadas em uma barra de massa desprezível que gira em torno do eixo $\mathcal{O}$ com velocidade angular $\omega$, conforme a figura.
2$^{\rm a}$ Questão (1,0 ponto): Considere os vetores unitários conforme a Figura 1. Para desacelerar o conjunto de massas $m_1$, $m_2$ e $m_3$ é necessário realizar um torque na direção
(a) $\hat{i}$ (b) $\hat{j}$ (c) $\hat{k}$ (d) $-\hat{i}$ (e) $-\hat{j}$ (f) $-\hat{k}$
R.: (f)
Questões de 2017.1¶
A Figura 2 a seguir mostra um objeto uniforme que rola sem deslizar sobre um plano inclinado. O objeto possui massa $M$, raio $R$ e momento de inércia $I_1$ ao redor do eixo de rotação. Sabe-se que quando o objeto é liberado do repouso a partir de uma certa altura $H$, ele é lançado horizontalmente ao chegar à base do plano inclinado, tocando o solo a uma distância horizontal $d_1$ do ponto de lançamento.
3$^{\rm a}$ Questão (1,0 ponto): Considere, agora, que o objeto é substituído por outro, de mesma massa $M$, mesmo raio $R$ e momento de inércia $I_2 > I_1$ ao redor do eixo de rotação. Nesse caso, quando solto do repouso da mesma altura $H$, o novo objeto rola sem deslizar, e toca o solo a uma distância $d_2$ do ponto de lançamento. Pode-se afirmar que:
(a) $d_1$<$d_2$ (b) $d_1=d_2$ (c) $d_1$>$d_2$ (d) Os dados são insuficientes para relacionar $d_1$ e $d_2$.
R.: (c)
Questões de 2017.1¶
A Figura 2 a seguir mostra um objeto uniforme que rola sem deslizar sobre um plano inclinado. O objeto possui massa $M$, raio $R$ e momento de inércia $I_1$ ao redor do eixo de rotação. Sabe-se que quando o objeto é liberado do repouso a partir de uma certa altura $H$, ele é lançado horizontalmente ao chegar à base do plano inclinado, tocando o solo a uma distância horizontal $d_1$ do ponto de lançamento.
4$^{\rm a}$ Questão (1,0 ponto): Na iminência do lançamento horizontal o centro de massa do cilindro possui uma velocidade $v_{cm} = 3,0$ m/s. Sabendo que o $R=0,50$ m, qual é o período $T$ de rotação do cilindro em torno de seu centro de massa?
Dado: considere $\pi\approx 3,0$.
(a) $T = 0,10$ s (b) $T = 0,30$ s (c) $T = 0,60$ s. (d) $T = 1,0$ s (e) $T = 1,8$ s (f) $T = 2,4$ s.
R.: (d)


