Amplificador diferencial
FI577 - Instrumentação eletrônica para a física
Leituras recomendadas: Horowitz & Hill Cap. 2
Amplificador Emissor Comum
- Vimos que o ganho de tensão do AEC é
- Ganho de tensão: \(A_V=-\frac{R}{R_E}\)
- O que acontece se \(R_E=0\)?
- O modelo simplificado que estamos utilizando para o transistor falha!
- Precisamos de um modelo mais sofisticado
Aprimorando o modelo do transistor
- Efetivamente, existem diodos entre a base e o coletor e o emissor
- Podemos considerar também em detalhes as correntes que passam entre os terminais
- No caso de um transistor NPN, conforme o circuito ao lado
- Caso mais geral
Transistor em estado ativo
- Devido ao diodo, a corrente \(I_E\) pelo emissor está relacionada com a tensão entre a base e o emissor
- \(I_E = I_{ED} = I_{E0} \left(e^{\frac{V_{BE}}{V_T}}-1\right)\)
- A corrente que entra pelo coletor, \(I_C\), é proporcional à corrente do diodo
- \(I_C = \alpha_F I_{ED}\), (\(\alpha\approx 1\))
- A corrente na base é a restante
- \(I_C + I_B = I_E\), ou \(I_B = (1-\alpha)I_E\)
- A corrente pelo emissor é exponencial em \(V_{BE}\)!
Cálculo
- Vimos anteriormente que o diodo pode ser considerado num circuito em termos de dispositivo ideal que controla o fluxo de cargas em série com uma fonte de tensão (0,6 V)
- Vimos ainda que era possível melhorar este modelo, incluindo uma resistência em série
- Como podemos determinar esta resistência \(r_E\)? Manipulando as expressões anteriores, temos
- \(V_{BE} = V_T \log \left(\frac{I_E}{I_{E0}} + 1 \right)\)
- Considerar que, na média, temos \(I_C=1\text{ mA}\approx I_E\).
- Se a corrente \(I_E\) variar pouco, teremos que a tensão \(V_{BE}\) também varia um pouco.
- \(V_{BE} + \Delta V_{BE} = V_T \log \left(\frac{I_E + \Delta I_E}{I_{E0}} + 1 \right)\)
- Podemos definir uma resistência equivalente ao analisar a relação entre \(\Delta V_{BE} = r_E \Delta I_E\)
Resistência equivalente
- \(V_{BE} + \Delta V_{BE} = V_T \log \left(\frac{I_E + \Delta I_E}{I_{E0}} + 1 \right)\)
- Série de Taylor: \(F(x+a)\approx F(a) + F'(a) x + F''(a) \frac{x^2}{2} + \dots\)
- Então \(\Delta V_{BE} = \frac{d V_{BE}}{dI_E} \Delta I_E\), ou \[r_E=\frac{d V_{BE}}{dI_E} = \frac{V_T}{I_E + I_{E0}}\]
- Considerando que \(V_T=25\text{ mV}\), pode-se reexpressar \(r_E\) como \[r_E = \frac{25}{I_E} \, \Omega \] onde \(I_E\) está expresso em mA.
- Logo, para uma corrente de 1 mA, existe uma resistência efetiva de 25 \(\omega\)
- Quanto maior a corrente, menor a resistência efetiva
Amplificador Emissor Comum
- Retornando ao AEC…
- Ganho de tensão: \(A_V=-\frac{R}{R_E}\)
- O que acontece se \(R_E=0\)?
- Existe uma resistência efetiva em série com o emissor, \(r_E\approx 25\,\Omega\)
- Ganho máximo: \(A_V=-\frac{R}{r_E}\)
Espelho de corrente
- Uma forma de aumentar a faixa de compliance
- Transistores PNP
- Notar que este circuito só faz sentido se considerarmos o modelo de Ebers-Moll!

Amplificador diferencial
- Até aqui vimos que é possível usar os transistores como amplificadores
- É bastante comum tentar extrair sinais pequenos de dentro de grandes ruídos
- Ex.: Eletrocardiograma
- A extração destas informações costuma usar um amplificador diferencial
- Rejeita sinais comuns (caracterizada pela Common mode rejection ratio) e amplifica a diferença entre os terminais.
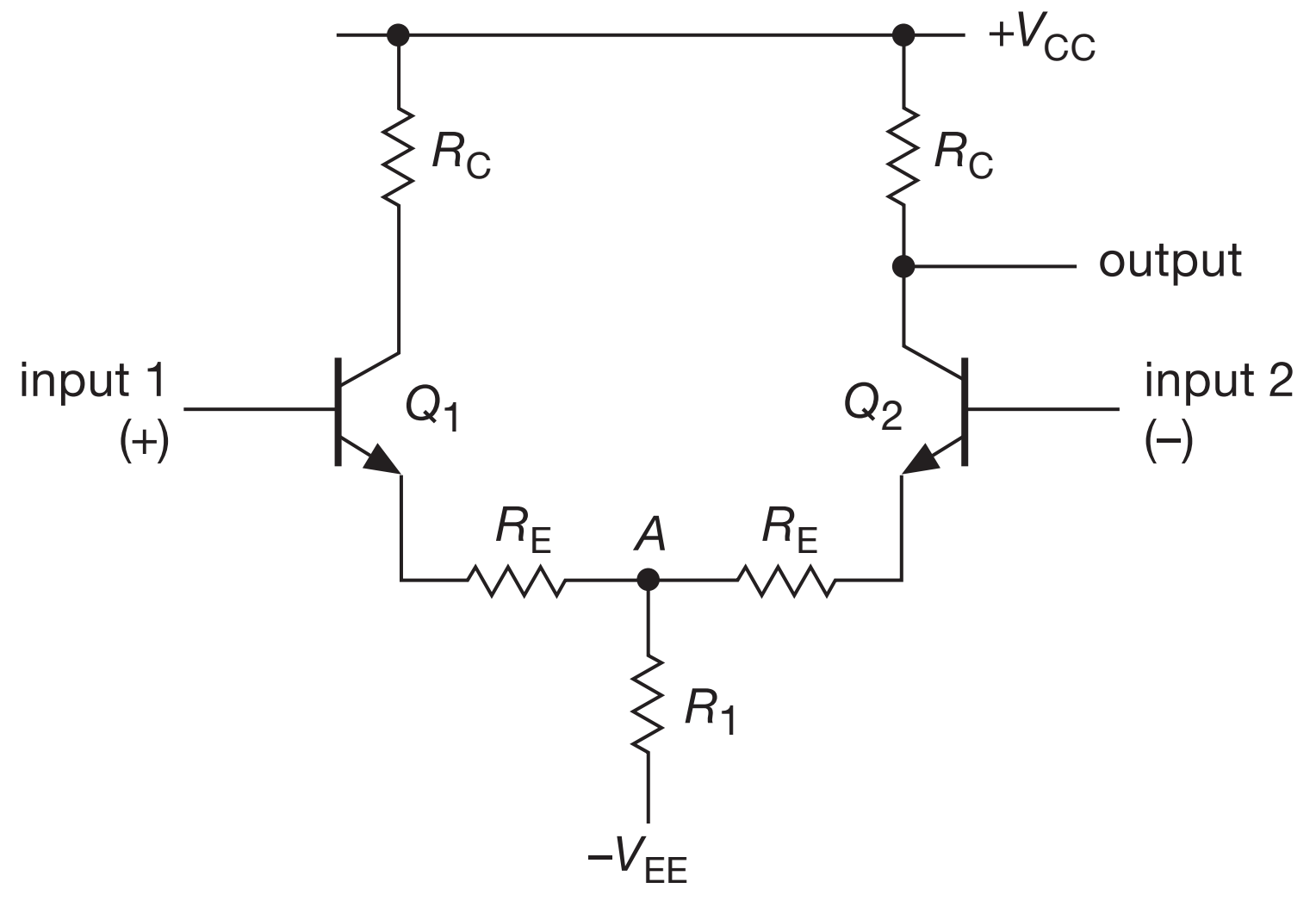
Parâmetros
- De forma mais usual, temos 2 entradas (+ e -) uma única saída
- \(R_1\) é grande (~k\(\Omega\)) enquanto \(R_E\) é pequeno (~\(100\,\Omega\))
- Ganho do modo comum: \(G_{CM} = - \frac{R_C}{R_E+2R_1}\)
- Ganho diferencial: \(G_{diff} = \frac{R_C}{2(r_e+R_E)}\)
- Razão de rejeição do modo comum: \(CMRR=\frac{R_1}{2(r_e+R_E)}\)

Fonte de tensão simétrica
- bullets
- items