Amplificador operacional

FI577 - Instrumentação eletrônica para a física

Leituras recomendadas: Agarwal Cap. 15 e Horowitz & Hill Cap. 4

Amplificação e controle

Vimos anteriormente que é possível utilizar transistores para amplificar sinais, utilizando o terminal da base como controle de sinais.
Como podemos realizar operações matemáticas sobre os sinais que estamos utilizando (\(+, -, \times, /\))?
Podemos usar os transistores diretamente, ou usar outro componente mais apropriado…
Amplificador operacional (Amp-Op): circuito integrado que simplifica a realização de diversas operações matemáticas
O aspecto chave que permite um bom funcionamento do Amp-Op é o seu alto ganho diferencial

O Amp-Op possui 2 entradas [inversora (-) e não inversora (+)].
A tensão na saída é dada por \(V_O=A\left(v_+-v_-\right)\). Amplifica a diferença entre as tensões das suas entradas.
O ganho \(A\) possui um valor muito grande (ex.: \(10^5-10^{10}\))
Estimativa: se \(\delta V=10\) mV, tipicamente \(V_O\geq10^3\) V! Considerando que a maior tensão do circuito é dada pela fonte de tensão, parece num primeiro momento que o Amp-Op é inútil por ter um ganho muito alto…
\(A\) possui o mesmo problema que o ganho de corrente de um transistor: não é um parâmetro confiável

A genialidade do Amp-Op está justamente em descartar o ganho excessivo, utilizando o sinal de saída para realimentar (feedback) uma das entradas.
Supor que \(v_-=B V_O\). Então, temos que \(V_O = \frac{A}{1+A B}v_+\).
Ora, \(A\) é muito grande… de forma que \(\frac{A}{1+AB}\approx \frac{1}{B}\).
\[V_O \approx \frac{v_+}{B}\]
A tensão na saída depende apenas dos componentes que utilizamos para a realimentação (B), que são parâmetros bem comportados.
Desde que vejamos como “construir” B’s adequados, podemos realizar diversas operações sobre \(v_+\).

Podemos também pensar em utilizar o sinal de saída para realimentar \(v_+\).
\(v_+=B V_O\). Então, temos que \(V_O = -\frac{A}{1-A B}v_-\).
Aparentemente o mesmo argumento anterior funcionaria, mas note que se \(A B = 1\), o circuito apresentará um comportamento singular.
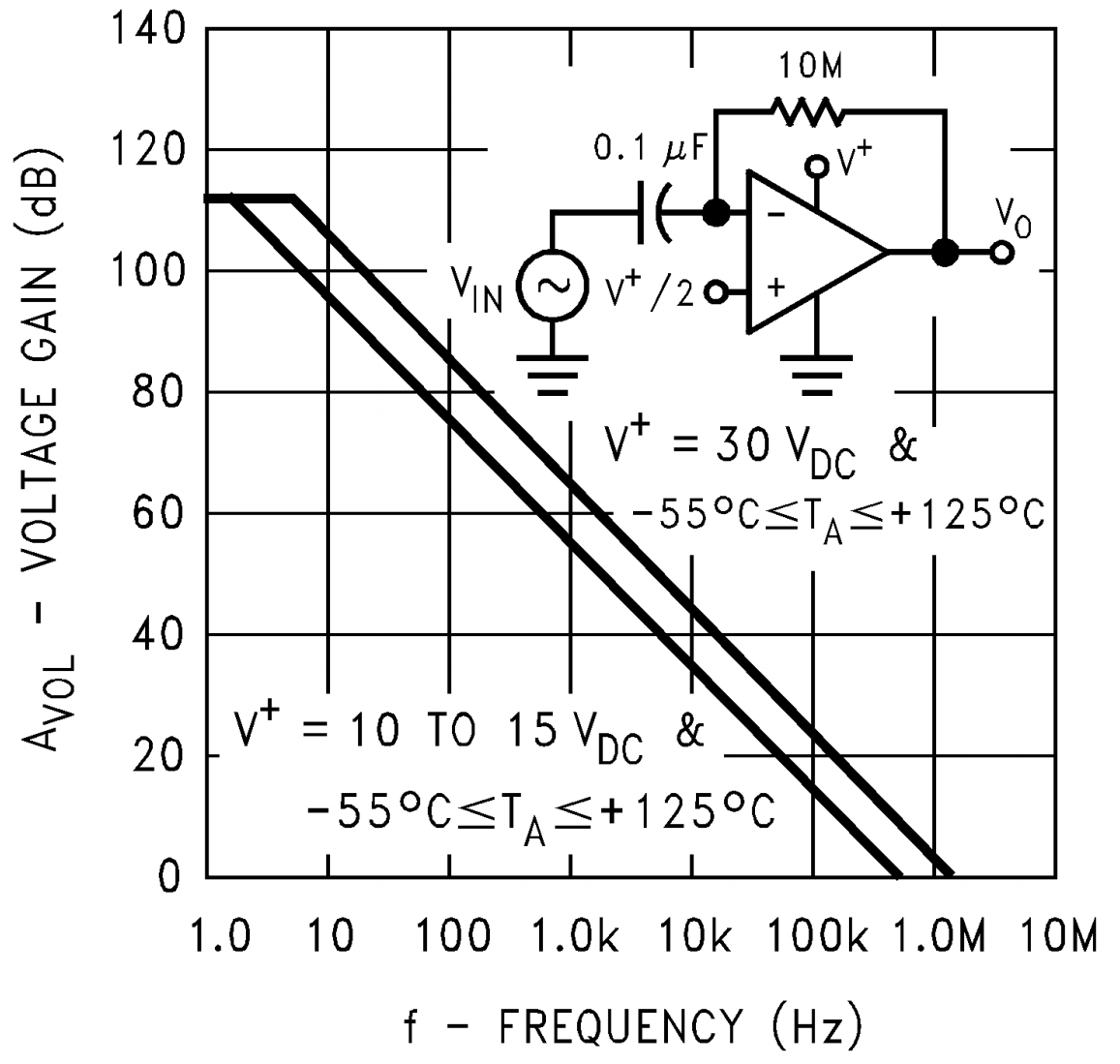
De fato, o ganho \(A\) varia com a frequência, de forma que existe uma frequência \(\omega_{GBP}\) tal que \(A=1\)
\(\omega_{GBP}\): Unity Gain-Bandwidth Product frequency
A realimentação positiva geralmente produz um circuito instável, sujeito a oscilações.

LM324

\(V_O=A\left(v_+-v_-\right)\)
Notar que, se o Amp-Op está funcionando adequadamente (usando realimentação negativa), temos que \(V_O\) é uma tensão limitada pela fonte de tensão usada no sistema (ex.: \(-9 \leq V_0 \leq 9\)). Ou seja, \(v_+-v_-=\frac{V_O}{A}\approx 0\)

Curto circuito virtual: \(v_+=v_-\)
Usando realimentação negativa, o Amp-Op força com que as tensões \(v_+\) e \(v_-\) sejam iguais.
Além disso, a corrente que entra no Amp-Op é geralmente desprezível
\(I_+ = I_- = I_B\). Tipicamente, \(I_B\leq100\,\text{nA}\) quando o Amp-Op utiliza transistores bipolares na entrada, e \(I_B\leq100\,\text{pA}\) quando utiliza transistores CMOS e/ou FET.

\[V_{out} = \left(1+\frac{R_2}{R_1}\right) v_{in}\]
A tensão na saída é maior que na entrada! Notar também que a impedância da entrada é muito elevada.

Consideremos o circuito ao lado. Qual a relação entre \(v_{out}\) e \(v_{in}\)?
Pelo princípio do curto virtual, sabemos a tensão em \(v_-\). Sabemos ainda que não entra corrente pelo Amp-Op.
\(v_- = v_+ = 0\), e \(I_{in} = I_L\).
\(I_{in} = \frac{v_{in} - 0}{R_1} = I_L = \frac{0 - v_{out}}{R_2}\)

Podemos analisar também circuitos que contenham indutores e capacitores, substituindo as resistências nos casos anteriores por impedâncias. \(v_{out} = -\frac{Z_2}{Z_1} V_{in}\)
Suponha que \(Z_1 = R\), \(Z_2 = -j/\omega C\). Então, temos \[v_{out} = -\frac{1}{j\omega R C} V_{in}\]

A função de transferência é a mesma de um integrador ideal (Não precisamos trabalhar com sinais pequenos)
Suponha que \(Z_1 = -j/\omega C\), \(Z_2 = R\). Então, temos \[v_{out} = -j\omega R C V_{in}\]
A função de transferência é a mesma de um diferenciador ideal (Não precisamos trabalhar com sinais pequenos)

Podemos somar tensões usando o circuito ao lado, convertendo a soma de correntes em uma d.d.p.
\(v_- = v_+ = 0\), \(I_1 + I_2 = I_G\)
\(\frac{V_1-0}{R_1} + \frac{V_2-0}{R_2} = \frac{0-V_{out}}{R_G}\).
Se \(R_1=R_2=R\), \[V_{out} = -\frac{R_G}{R}\left(V_1+V_2\right)\]

E como realizar uma subtração?
Podemos modificar a tensão na entrada não invertida (sem incluir \(v_+\) na realimentação!)
\(v_+ = \frac{R_3}{R_2+R_3} V_2 = v_-\), \(I_1 = I_G\)
\(\frac{V_1-v_-}{R_1} = \frac{v_--V_{out}}{R_G}\).
\(\frac{V_1}{R_1} - \left(\frac{1}{R_1} + \frac{1}{R_G}\right) v_- = - \frac{V_{out}}{R_G}\)

\(V_{out} = -\frac{R_G}{R_1} V_1 + \frac{R_G+R_1}{R_G R_1} \frac{R_3}{R_2+R_3} V_2\)
Se \(R_1=R_2=R\) e \(R_3=R_G\), temos
\[V_{out} = \frac{R_G}{R} (V_2-V_1)\]
Podemos considerar a diferença entre 2 sinais, e mesmo amplificar esta diferença (\(R_G>R\))

Amp-Op’s melhoram a performance de filtros de sinais.
Consideremos um filtro passa baixa na topologia Sallen-Key
\(v_+=v_-=V_{out}\).
Correntes em \(V_X\): \(\frac{V_{in}-V_X}{R_1} = \frac{V_{X}-V_{out}}{R_2} + \frac{V_{X}-V_{out}}{-j/\omega C_1}\).

\(C_1\) e \(R_2\) virtualmente em paralelo.
A corrente que atravessa \(R_2\) também passa por \(C_2\): \(\frac{V_{X}-V_{out}}{R_2}=\frac{V_{out}}{-j/\omega C_2}\).
Resolvendo o sistema, encontramos \[V_{out} = \frac{V_{in}}{1 - \omega^2 R_1 R_2 C_1 C_2 + j \omega (R_1+R_2) C_2}\]
Notar a ressonância em \(\omega_0^2 R_1 R_2 C_1 C_2=1\), ou \(\omega_0=1/\sqrt{R_1 R_2 C_1 C_2}\) (existe feedback positivo!)