Eletromagnetismo

• Interação entre cargas e correntes (cargas em movimento).
• Carga elétrica \(Q\)
  • 2 tipos: positiva e negativa (\(Q_+\), \(Q_-\))
  • Num sistema isolado, a carga total é sempre conservada.
  • \(Q_+ + Q_- = \text{cte}\).
  • \(Q\) é um escalar (não possui informação sobre direção).

Lei de Coulomb, campo elétrico e energia

• Interações entre cargas estáticas
• Força sobre \(Q\) devido a \(q_1\): \(\vec{F}_{1}=k\frac{Q q_1 \hat{r}_{1,Q}}{r_{1,Q}^2}\)
• Se há várias cargas atuando, a força total é \(\vec{F}=Q \sum_i k\frac{q_i \hat{r}_{i,Q}}{r_{i,Q}^2}\), ou \[\vec{F}=Q \vec{E}\]
• \(\vec{E}\): Campo elétrico
• Estamos interessados em compreender alguns aspectos de cargas e correntes voltados a circuitos. Em especial, como podemos entender de maneira simples o que acontece quando uma carga sai de um ponto \(A\) até \(B\)?

Trabalho e energia potencial

• \(Q\) sai do ponto \(A\) e vai até \(B\) seguindo um dado caminho \(C\). Como varia sua energia potencial?
• Trabalho \(W = \int \text{Força}\times \text{Deslocamento} = \int_C Q\vec{E} \cdot d\vec{s}\)
• \(W = Q \int_C \vec{E} \cdot d\vec{s}\)
• Campo \(\vec{E}\) é conservativo, logo \(W = - \Delta U\) (o trabalho indica a variação do potencial \(U\)).
• Como \(Q\) é um escalar, podemos monitorar as variações de energia da \(Q\) ao observar as variações do potencial elétrico \[\Delta V=-\int_C \vec{E} \cdot d\vec{s}\]
• \(V\) conforme a definição acima pode ser usado sob circunstâncias razoavelmente gerais. Vocês conseguem identificar algo que pode atrapalhar o raciocínio acima?

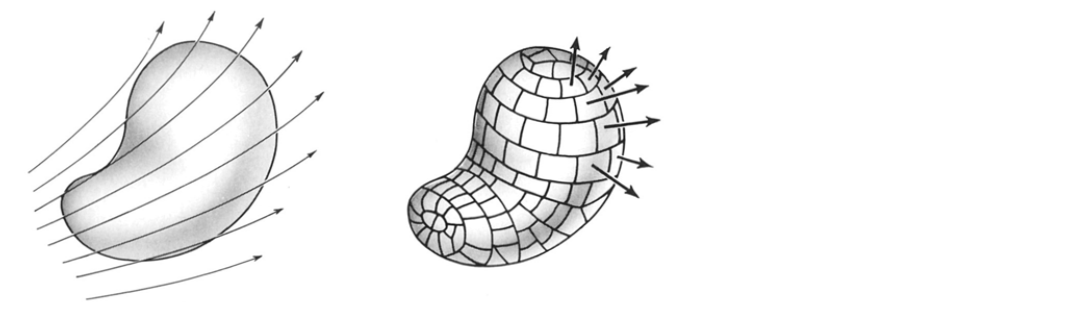
Fluxo de campo elétrico

• Que porção do campo elétrico \(\vec{E}\) atravessa uma dada superfície de área \(a\)?
• Seja \(\hat{a}\) normal a superfície, denomina-se fluxo como \[\vec{E}\cdot\vec{a}\]
• Fluxo por uma superfície fechada: \(\Phi = \sum_{\text{todos os }j} \vec{E}_j\cdot\vec{a_j}\).
• No limite quando as áreas tornam-se muito pequenas, \[\Phi = \int_{\text{toda a superfície}} \vec{E}\cdot\,d\vec{a}\]

Lei de Gauss

Placa infinita plana homogeneamente carregada

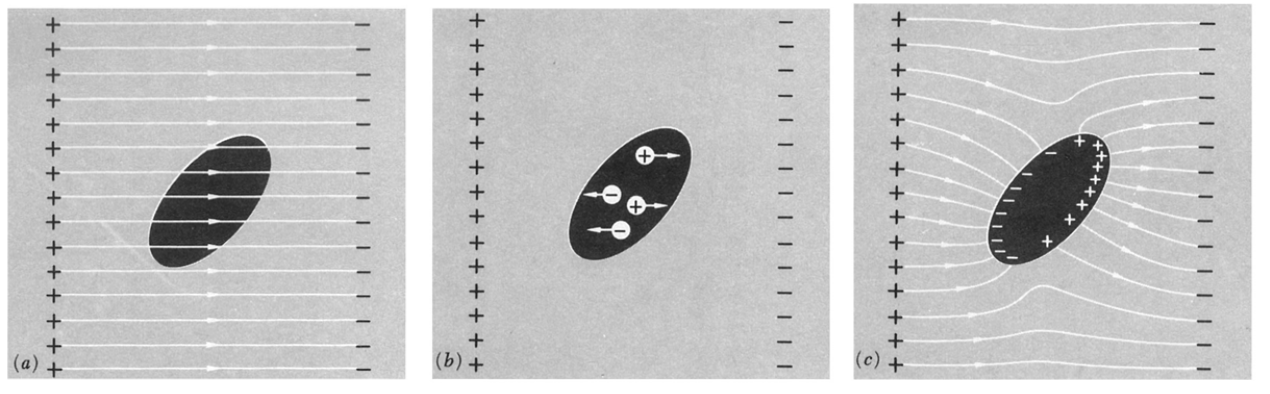
Condutores e isolantes num campo eletrostático

• O que ocorre ao inserir um material em uma região com um campo homogêneo?
• \(\vec{F} = q \vec{E}\): cargas positivas tendem a se mover ao longo da direção de \(\vec{E}\), e negativas no sentido oposto.
• Num isolante, o movimento das cargas é muito pequeno
• Num condutor, as cargas podem se mover livremente. Sob que condição o movimento cessa?
  • O campo elétrico é nulo dentro de um condutor ideal.
  • As cargas livres movem-se até a superfície.

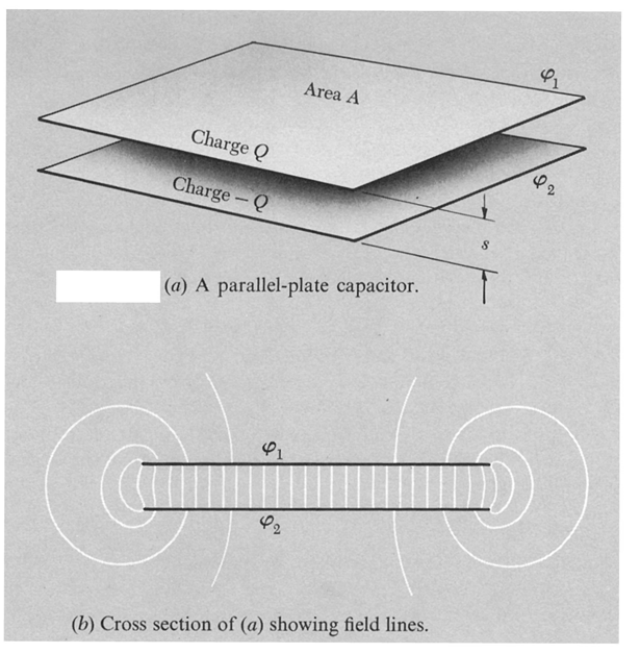
Capacitor

Energia armazenada num capacitor

• Capacitor com carga \(Q=CV\). Que trabalho é necessário para levar \(dQ\) de uma placa a outra?
• \(dW = V dQ = \frac{Q dQ}{C}\)
• Integrando desde quando o capacitor está descarregado, \(W = \frac{1}{C} \int_{Q=0}^{Q_f} Q dQ\)
• \(W = \frac{Q_f^2}{2C} = \frac{C V^2}{2}\).
• Importante: um capacitor pode ser visto como um reservatório de cargas elétricas ou de energia elétrica. Este comportamento será crucial em vários circuitos relevantes.

Corrente elétrica

• Para que os circuitos “façam algo”, precisamos das cargas em movimento.
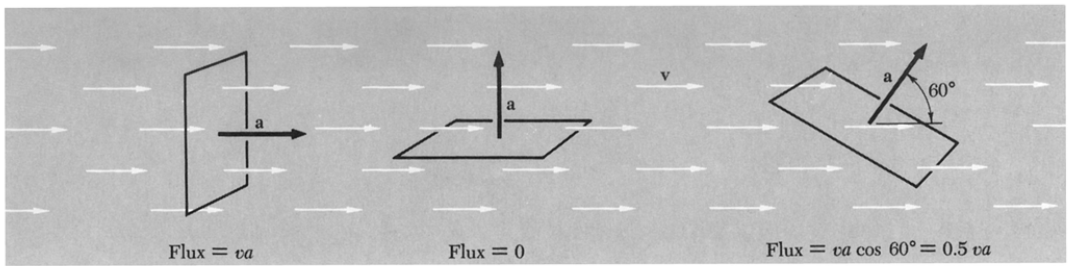
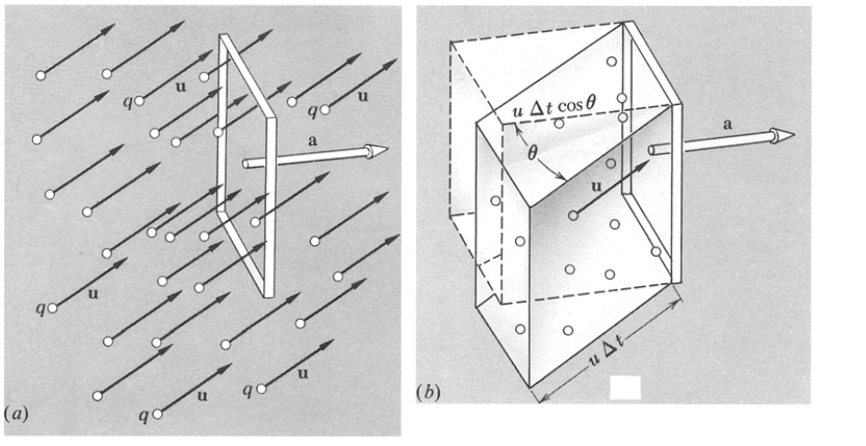
• Quanta carga atravessa uma dada região de área A [Fig. (a)]?
• Imagine \(n\) cargas \(q\) de velocidade \(\vec{u}\). Num tempo \(\Delta t\), o deslocamento é \(\Delta \vec{r} = \vec{u}\Delta t\).
• Notar que o deslocamento na direção da região de área \(A\) é dado \(u\cos\theta\), onde \(\theta\) é o ângulo entre \(\vec{u}\) e \(\vec{a}\).
• Carga que atravessa \(A\): \((n q) \vec{a}\cdot\vec{u}\Delta t\)
• A taxa média com que as cargas atravessam \(A\) é então
• \(I_a = \frac{(n q) \vec{a}\cdot\vec{u}\Delta t}{\Delta t} = (n q) \vec{a}\cdot\vec{u}\)

Densidade de corrente

• \(I_a = \frac{(n q) \vec{a}\cdot\vec{u}\Delta t}{\Delta t} = (n q) \vec{a}\cdot\vec{u}\)
• Caso haja vários tipos de partículas que podem atravessar \(A\) (ex.: íons, elétrons, prótons…), podemos separar a contribuição anterior para cada espécie de partícula \(k\)
• \(I_a = \vec{a} \cdot \sum_k n_k q_k \vec{u}_k\)
• Densidade de corrente \(\vec{J}=\sum_k n_k q_k \vec{u}_k\)
• \(J\) é especialmente importante quando se tem diversos tipos de portadores de carga (semicondutores, soluções iônicas, plasmas…), ou quando os portadores não possuem a mesma direção de propagação.

Densidade de corrente média

• Consideremos apenas um tipo de portador (ex.: elétrons), em que os \(N\) portadores de uma dada região podem possuir várias velocidades \(\vec{u}\) distintas. A velocidade média satisfaz
• \(N \bar{\vec{u}} = \sum_k n_k \vec{u}_k\), ou
• \(\bar{\vec{u}} = \frac{1}{N}\sum_k n_k \vec{u}_k\)
• Em termos de \(\bar{\vec{u}}\),
• \[\vec{J}= q N \bar{\vec{u}}\]

Correntes estáticas e conservação da carga

• A corrente que atravessa uma superfície \(S\) é \[I = \int_S \vec{J}\cdot d\vec{a}\]
• Fisicamente, o que esta corrente indica se \(S\) é uma superfície fechada?
• \(I\) indica - a variação da carga líquida armazenada em \(S\). \[\int_S \vec{J}\cdot d\vec{a} = - \frac{dQ}{dt}\]
• A relação acima indica a conservação total da carga elétrica.

Condutividade elétrica

• Como relacionar o movimento dos portadores de carga em um dado material com o campo elétrico em uma dada região?
• Usualmente observa-se que vale a lei de Ohm, \[\vec{J} = \sigma \vec{E},\] onde \(\sigma\) é a condutividade do material.
  • Lei empírica, válida em muitos casos (mas nem sempre!).
  • Falha p. ex. em filamentos aquecidos.
  • Lembrar que \(\vec{J}= q N \bar{\vec{u}}\). Tipicamente, \(\bar{\vec{u}}\propto \vec{E}\).
  • Em alguns materiais \(\sigma\) pode depender também da orientação dos campos relativamente ao material. Ex.: grafeno.

Lei de Ohm em termos da tensão

• Supor que uma corrente \(I\) atravessa um paralelepípedo de comprimento \(L\), área transversal \(A\) e condutividade \(\sigma\). Supor ainda que o campo \(\vec{E}\) é uniforme dentro do material.
  • \(J = I/A\)
  • \(E = V/L\)
  • Usando a lei de Ohm, \(J = \sigma E\), temos \[V = R I\]
    • \(R = \frac{V}{I} = \frac{L}{\sigma A}\)
    • É usual também falar em termos da resistividade \(\rho=\sigma^{-1}\), e
    • \(R = \frac{\rho L}{A}\)

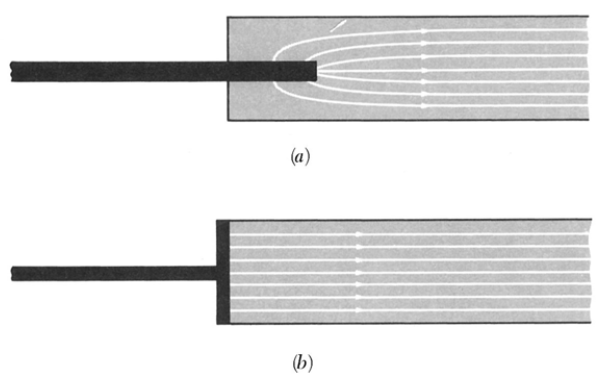
• Perceba que no modelo acima ignoramos diversos detalhes da configuração dos campos dentro do material Ôhmico.
• Dependendo de como é o condutor que injeta a carga no material ôhmico, o campo elétrico pode ser inhomogêneo dentro do material.

Aspectos físicos da condução elétrica

• Materiais são eletricamente neutros.
• Os portadores de carga possuem algum tipo movimento (pois \(T\neq 0\) K), mas que na média não possui qualquer direção preferencial. Por que?
• O que acontece quando um campo \(\vec{E}\) é aplicado?
• A partícula carregada será acelerada na direção do campo.
• E o que acontece após a remoção do campo \(\vec{E}\)?
• O portador deve reduzir sua velocidade devido a colisões dentro do material.

• Modelo simples:
• Portador possui momento \(m \vec{u}_c\) após a última colisão.
• Acelera devido a \(\vec{E}\) num tempo \(t\): \(\Delta \vec{p} = q \vec{E} t\)
• Momento total após um tempo \(t\): \(m \vec{u}_c + q \vec{E} t\)
• Se \(\vec{E}\) não é muito grande, o tempo \(\tau\) entre colisões não muda muito em relação à quando o material não possui campo aplicado.
• Momento total de \(N\) portadores: \[ M\vec{u} = \frac{1}{N} \sum_{k} \left( M \vec{u}_c + q \vec{E} \tau \right)\]

• Momento total de \(N\) portadores: \[ M\vec{u} = \frac{1}{N} \sum_{k} \left( M \vec{u}_c + q \vec{E} \tau \right)\]
• Mas, como a velocidade média se anula na ausência de campo aplicado, \(M\vec{u} = q \vec{E} \tau\)
• Ou seja, \[ \vec{u} = \frac{q \vec{E} \tau}{M} \]
• A densidade de corrente satisfaz \[\vec{J} = q N \bar{\vec{u}} = \frac{q^2 N \tau}{M} \vec{E}\]
• Condutividade \[\sigma = \frac{q^2 N \tau}{M}\]

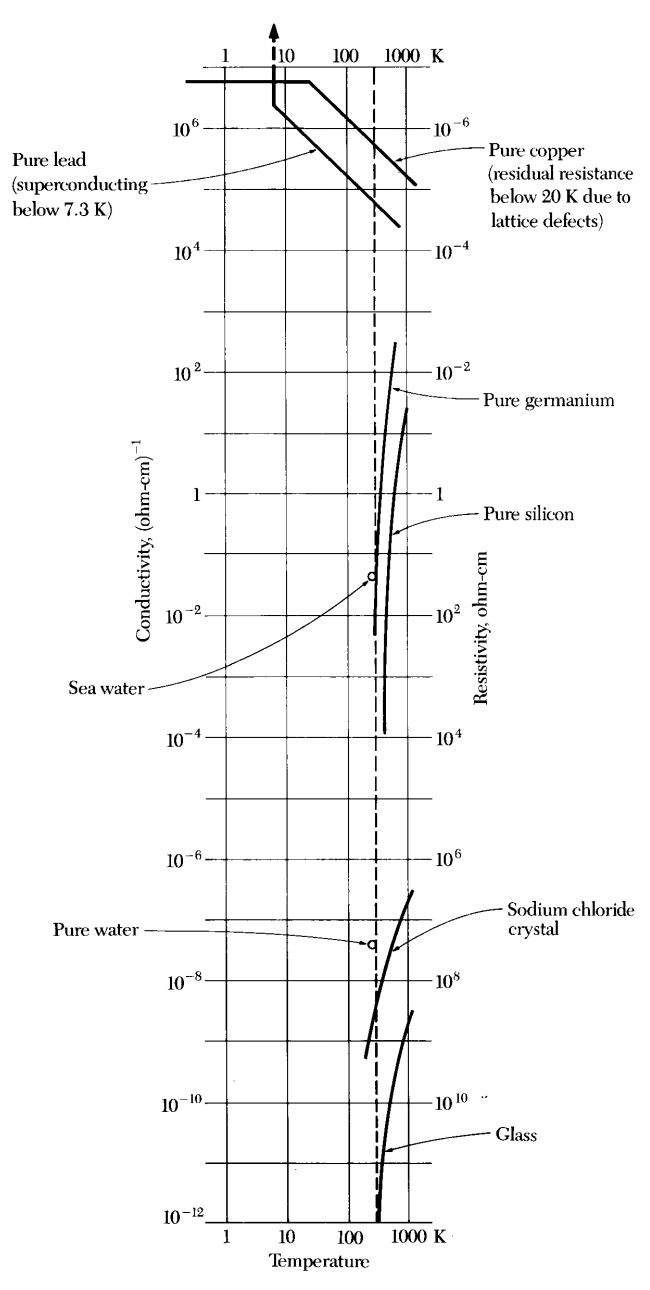
Condução em metais

• Possuem elétrons fracamente presos aos átomos
• Íons positivos + nuvem de elétrons
• 1+ elétrons de condução por cada átomo do material
• \(~10^{22}\) portadores por cm\(^3\)

Condução em semicondutores

• Ex.: Silício possui 4 elétrons de valência
• Forma ligações covalentes bastante estáveis com vizinhos.
• Em uma temperatura \(T=0\) K, todos os elétrons estão presos aos átomos. É um isolante ideal.
• Energia necessária para remover 1 \(e^-\) para a banda de condução: gap 1.12 eV.

• Se 1 \(e^-\) é promovido para a banda de condução, cria-se 2 portadores de carga efetivos:
  • O elétron, de carga - na banda de condução
  • A vacância do elétron, de carga +, na banda de valência. A vacância está associada a um movimento coletivo dos elétrons na banda de valência
• Com o aumento da temperatura, é possível em \(T>0\) K que alguns elétrons sejam promovidos para a banda de condução.
• Para o silício puro a temperatura ambiente, existem cerca de \(10^{10}\) elétrons e vacâncias de condução. É praticamente um isolante, se comparado a um metal típico.

Dopagem de semicondutores

• Portadores podem ser gerados por aquecimento, mas também pela introdução de impurezas.
• Suponha que \(10^{15}\) átomos/cm\(^3\) de Si são substituidos por fósforo (P), que possui 5 elétrons de valência.
• “Sobra” 1 elétron do fósforo, que não participará de ligações químicas.
• Neste processo, tem-se a geração de um íon positivo (P) e um elétron que pode se locomover no material.
• Tem-se agora cerca de \(10^{15}\) portadores de carga negativa/cm\(^3\)
• Dopagem tipo ‘N’

Dopagem de semicondutores

• Pode-se fazer o mesmo procedimento com outros dopantes.
• Ex.: Al possui 3 elétrons na banda de valência. O Al vai remover 1 elétron dos átomos vizinhos devido às 4 ligações, o que cria uma vacância na banda de valência.
• Dopagem tipo ‘P’

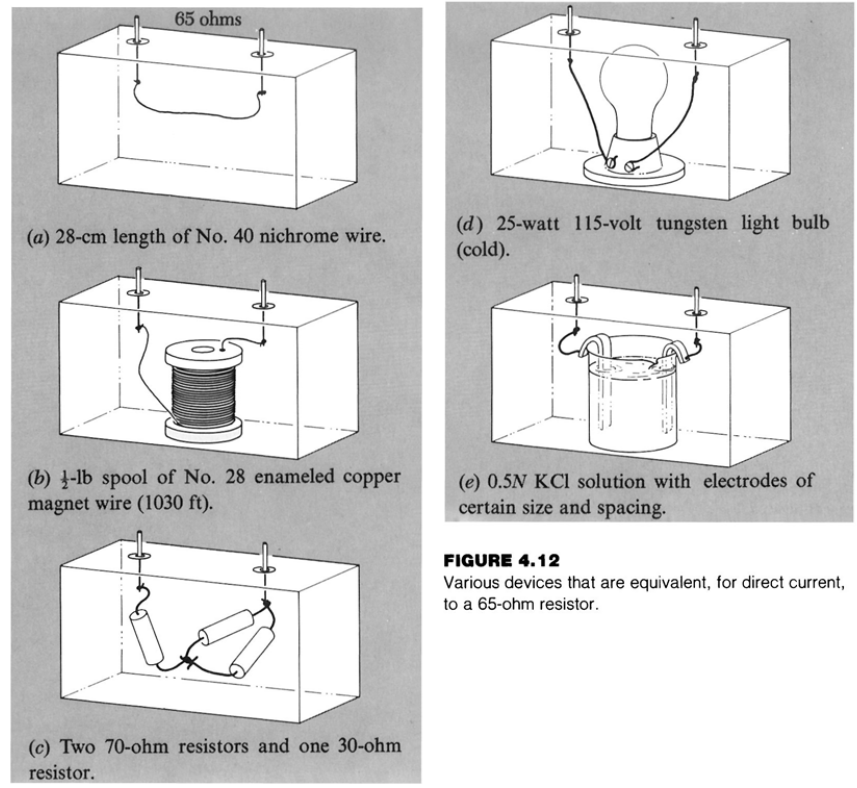
Circuitos e elementos de circuitos

• O que tem dentro da caixa?