Abstração de circuitos eletrônicos
FI577 - Instrumentação eletrônica para a física
Leitura recomendada: Agarwal (Caps. 1)
O poder da abstração
- Simplificação de conceitos para discutir os aspectos essenciais
- Ex.: como determinar as condições em que uma colisão ocorreu?
- Leis de Newton para partículas pontuais!
- Há pouca relevância nos detalhes internos do funcionamento dos veículos (peças, materiais, componentes…).
- Pode-se proceder de forma análoga para a compreensão de circuitos eletrônicos.

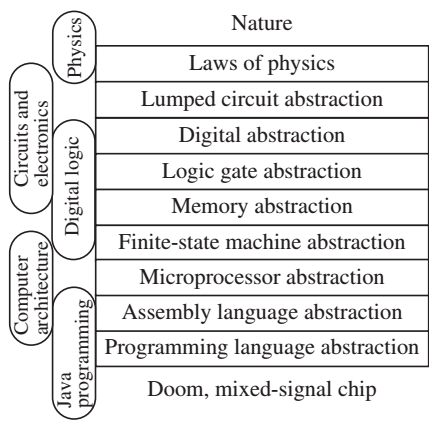
Camadas de abstração
- A segmentação do conhecimento em camadas de abstração permite a realização de tarefas cada vez mais complexas
- Especialmente interessante para instrumentação!
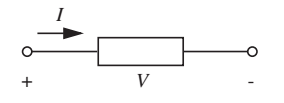
Circuitos e elementos de circuitos
- O que tem dentro da caixa? Em uma primeira análise, não nos importa
Exemplo
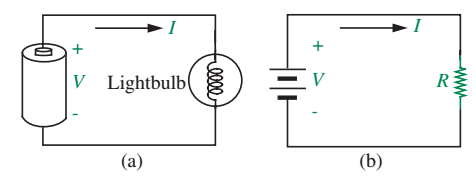
- A bateria possui uma diferença de potencial entre seus terminais. Fios conectam a bateria à lâmpada.
- Aspectos essenciais: tensão da bateria e resistência a passagem de corrente pela lâmpada.
- Aspectos não essenciais: material e dimensões do filamento utilizado, conexões elétricas, posição dos componentes…
- Podemos criar um elemento ideal para representar as propriedades elétricas essenciais da lâmpada
- Resistência da lâmpada: \(R = V/I\)
Abstração de parâmetros concentrados
- Um elemento a parâmetro concentrado equivale a uma caixa preta acessível apenas via alguns terminais.
- O que acontece nos terminais é mais importante que os detalhes internos
- A caixa-preta é uma camada de abstração entre o usuário e a estrutura interna da lâmpada
- Deve-se associar uma tensão e uma corrente para cada terminal. Consideraremos principalmente elementos de 2 e 3 terminais.
Abstração de parâmetros concentrados
- A operação de um elemento a parâmetro concentrado depende apenas das tensões e correntes em seus terminais.
- Abstração de circuito a parâmetros concentrado: um circuito que obedece ao regime de matéria concentrada e composto por elementos a parâmetros concentrados e conectado por fios ideais resulta na abstração a circuitos concentrados
- Análoga a simplificação de partículas pontuais nas leis de Newton. Os detalhes internos são considerados irrelevantes.
- Saímos das Eqs. de Maxwell para usar relações algébricas mais simples.
Regime de parâmetros concentrados
- Elemento de 2 terminais:
![]()
- Características determinadas apenas pela tensão e corrente
- Quando podemos considerar um circuito como composto apenas por elementos de parâmetros concentrados?
- Precisamos partir das Eqs. de Maxwell, para encontrar as restrições associadas a esta simplificação.
R1 - Fluxo magnético
- Havíamos visto anteriormente que para um caminho \(P\) aberto vale aproximadamente a relação \(\Delta V = -\int_P \vec{E}\cdot d\vec{l}\).
- Sabe-se da lei da indução de Faraday que para um caminho \(C\) fechado, \[\int_C \vec{E}\cdot d\vec{l} = -\frac{d\Phi_B}{dt},\] onde \(\frac{d\Phi_B}{dt}\) é o fluxo de campo magnético por uma superfície com bordas em \(C\).
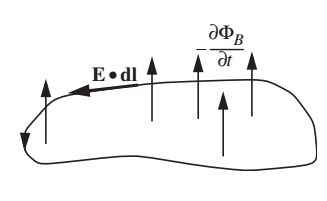
- Para definir uma tensão única entre os terminais, precisamos ter \[\frac{d\Phi_B}{dt} = 0\] em quaisquer caminhos externos ao elemento.
- Então esta discussão exclui indutores?
R2 - Carga total
- Havíamos visto anteriormente que \(I = \int_A \vec{J}\cdot d\vec{a}\) indica a corrente que atravessa uma superfície de área \(A\).
- Para uma superfície fechada \(S\) temos \(\int_S \vec{J}\cdot d\vec{a} = - \frac{dQ}{dt}\), onde \(Q\) é a carga dentro de \(S\)
- Para definir uma corrente única entre os terminais, precisamos ter \[\frac{dQ}{dt}=0\]
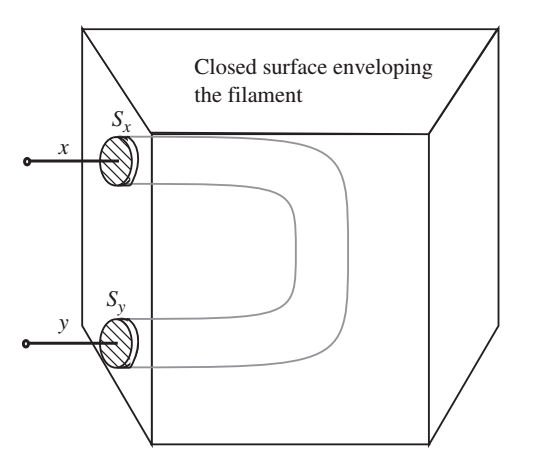
- Então esta discussão exclui capacitores?
R3 - Dimensões
- Outra limitação está associada com as dimensões do circuito.
- Em geral, \(V=V(t)\) e \(I=I(t)\). Se o circuito é grande o suficiente para que a velocidade finita de propagação dos sinais seja relevante, as tensões e correntes dependem do caminho seguido.
- Para que tais efeitos sejam irrelevantes, se \(\lambda = c/f\), onde \(f\) é a maior frequência de um sinal presente num sistema, as dimensões do circuito devem ser muito menores que \(\lambda\)
- Dimensões características para \(f=1\text{ kHz}, 1\text{ MHz}, 1\text{ GHz}\)?
- Quando a dimensão do circuito é \(~\lambda/10\) ou maior, precisa-se considerar efeitos de linha de transmissão, e deve-se usar o conceito de circuito com parâmetros distribuidos.
Elementos de 2 terminais
- Satisfeitas as condições anteriores, podemos representar um circuito em termos de elementos discretos.
- Elementos de 2 terminais estão entre os mais importantes. Ex.: Resistor, capacitor, indutor, baterias e fontes de tensão, diodos…
- Veremos alguns exemplos a seguir
Baterias
- Especificações mais importantes: tensão nominal, energia armazenada e resistência interna.
- Potência fornecida: \(P=\frac{dW}{dt}=\frac{dq V}{dt} = VI\)
- Ocorre quando \(I\) sai pelo terminal positivos
- Energia fornecida num tempo \(T\): \(E=PT\)
- Energia armazenada costuma ser representada em Ampére-hora ou Watt-hora.
- Quem possui mais energia armazenada, uma bateria de Níquel-Cádmio de 6V e 950 mA-hora, ou uma de íons de lítio de 7,2 V e 900 mA-hora?
Resistores
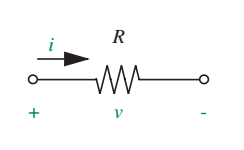
- Um resistor possui uma relação bem determinada entre a tensão e a corrente instantâneas entre seus terminais.
- Resistor linear: \(V(t) = I(t) R(t)\)
- Resistor linear e temporalmente invariante: \(V(t) = R I(t)\)
- Resistor não linear: \(V(t) = K I(t)^3\)
- Nota: capacitores e indutores não possuem relações instantâneas entre tensão e corrente

Convenção das variáveis associadas
- Definição: a corrente entra pelo terminal com a tensão mais positiva.
- A potência aplicada no elemento é positiva para \(V\) e \(I\) positivas.
- Resistor dissipa uma potência \(V I>0\)
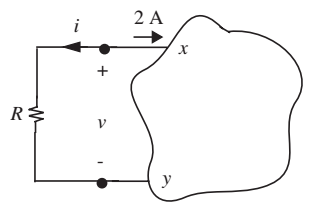
Exemplo
Considere o resistor na figura ao lado, conectado a um circuito nos pontos \(x\) e \(y\). Suponha que passa uma corrente de 2A pelo terminal \(x\).
- Qual o valor de \(i\)? -2 A
- Se \(R=10\Omega\), qual o valor de \(v\)? -20 V
Alguns componentes de 2 terminais ideais
- Fio ideal (curto circuito): \(R=0\), ou \(v=0\)
- Circuito aberto: \(R=\infty\), ou \(i=0\)
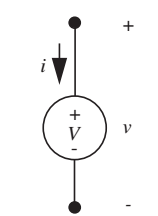
- Fonte de tensão ideal: \(v=V\)
- Mais adiante veremos qual a diferença entre uma fonte de tensão ideal de uma fonte real.
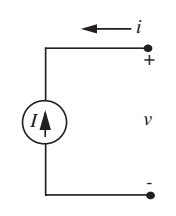
Fontes de corrente ideais
- Da mesma forma que podemos definir um componente de 2 terminais que fixa uma tensão entre seus terminais, pode-se especificar um componente que fixa uma corrente.
- Neste caso, \[i=I\].
- Elemento dual à fonte de tensão.
- Poucos componentes se comportam naturalmente como fontes de corrente (ex.: fotodiodos)
- Podem ser confeccionadas (faremos mais adiante!)
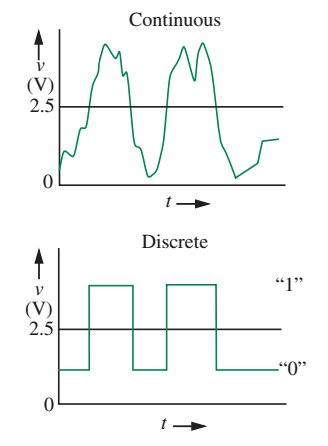
Sinais analógicos e digitais
- Grande parte das grandezas podem assumir “valores contínuos”. Ex.: distância, tempo, amplitude de uma onda sonora…
- Sinais analógicos
- Vantagem: processamento do sinal pode ser realizado em tempo real facilmente
- Desvantagens: mais suscetível a ruído, e é difícil de realizar modificações
- Existem também grandezas que assumem apenas valores discretos
- Sinais digitais.
- Vantagens: virtualmente imune a ruído, fácil de ser modificado
- Desvantagem: o processamento do sinal é bem mais lento