Análise de circuitos lineares
FI577 - Instrumentação eletrônica para a física
Leitura recomendada: Agarwal (Caps. 2 e 3)
Terminologia
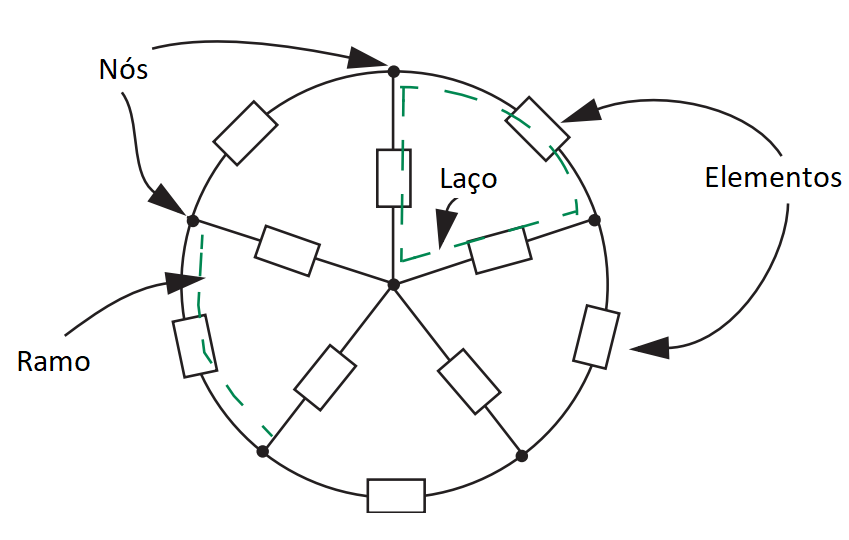
Terminologia
- Os terminais em um nó distribuído estão a um mesmo potencial. (Tensão do nó)
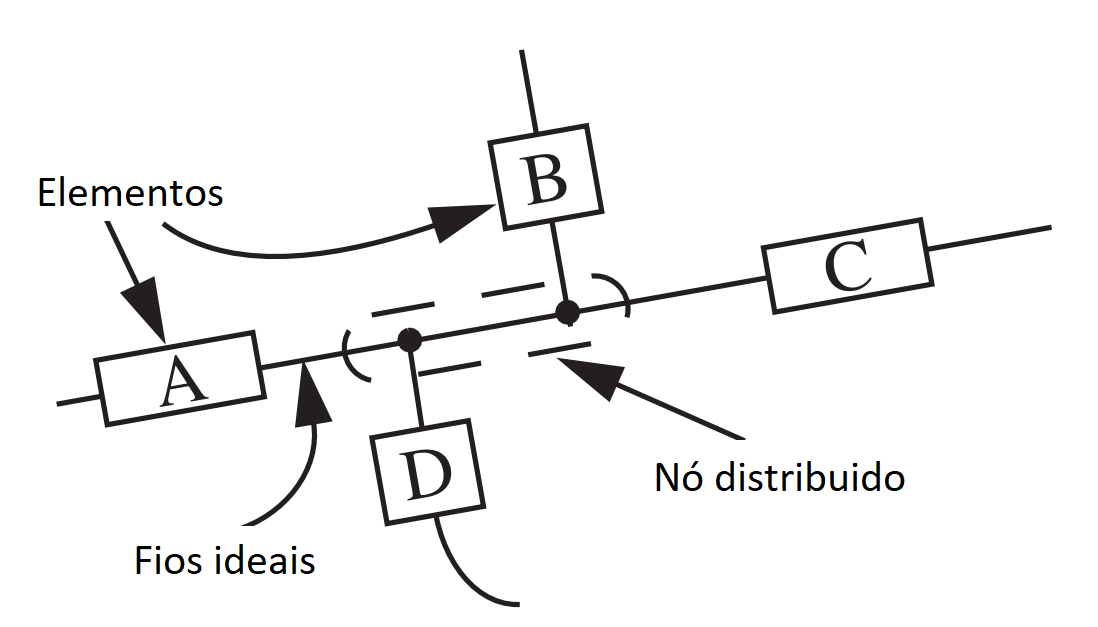
Terminologia
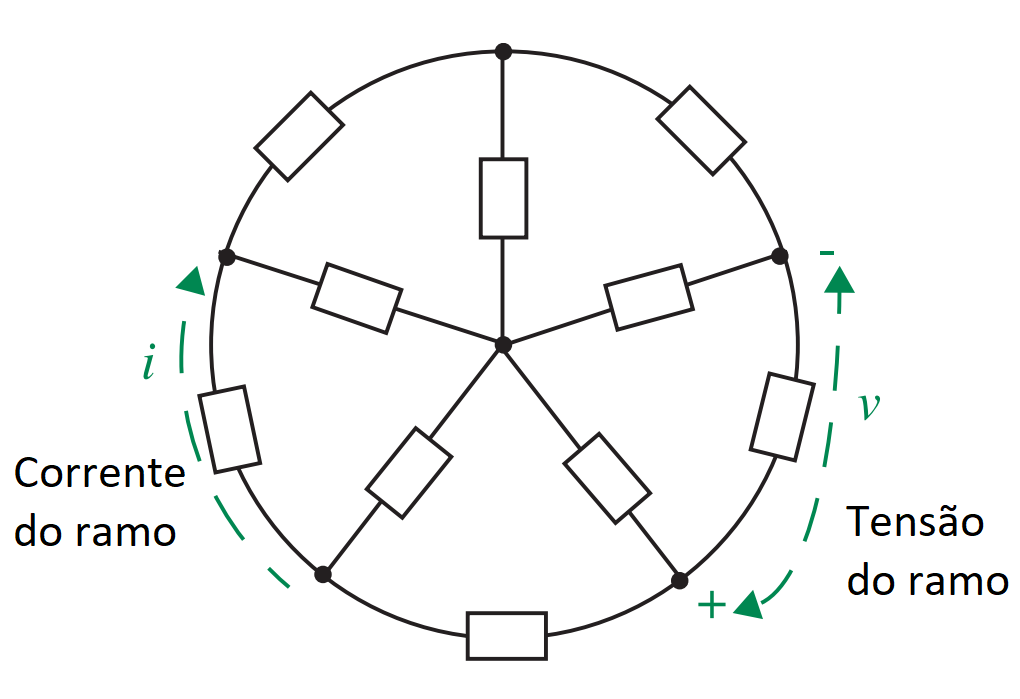
Leis de Kirchhoff
- Simplificações algébricas das Eqs. de Maxwell
- Lei das correntes: A soma das correntes que entram em um nó é igual a soma das correntes que saem. A soma das correntes por um nó deve ser nula.
- \(\int_S \vec{J}\cdot d\vec{a} \propto \frac{dQ}{dt} = 0\)
![]()
- \(i_a+i_b+i_c=0\)
Exemplo
- Qual o valor de \(i_2\)? \(i_2=-4\text{ A}\)
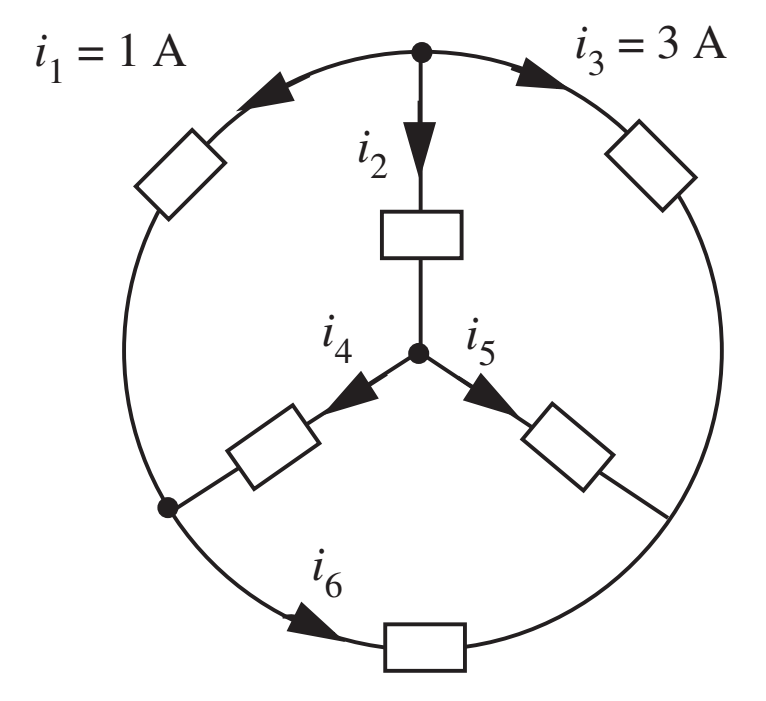
Exemplo
- Qual o problema com o circuito abaixo? A soma das correntes que entram/saem de cada nó não é nula e \(\frac{dQ}{dt} \neq 0\). Você consegue imaginar o que ocorreria numa situação real?
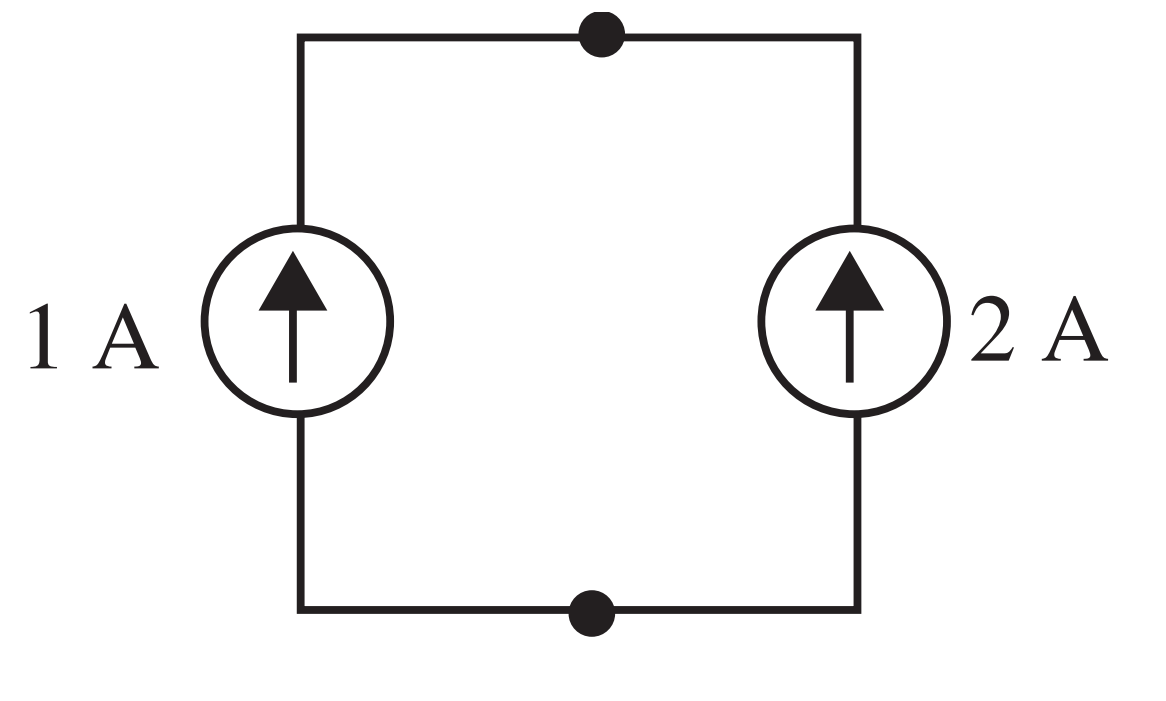
Leis de Kirchhoff
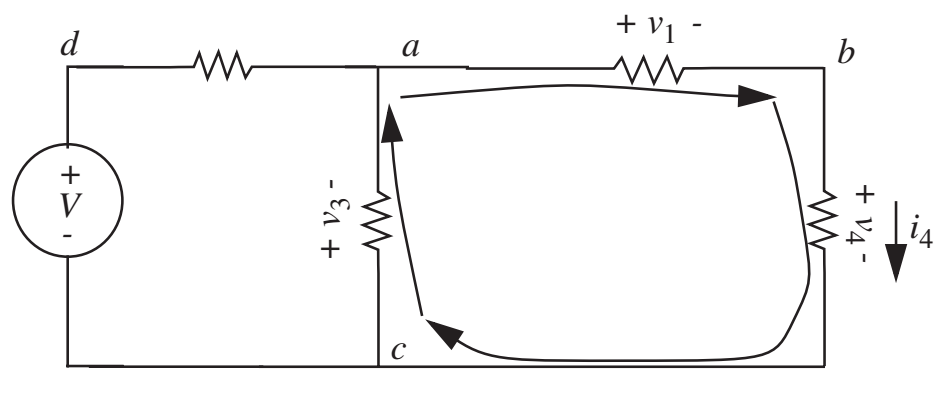
- Lei das tensões: A soma algébrica das tensões dos ramos através de qualquer caminho fechado (laço) em uma rede deve ser nula. A tensão entre dois nós independe do caminho.
- \(\Delta V = -\int_P \vec{E}\cdot d\vec{l}\). Campo \(\vec{E}\) é conservativo.
![]()
- \(v_1+v_4+v_3=0\)
- É importante ter cuidado com os sinais das tensões!
- Atribuir terminais \(+\) e \(-\) dos elementos. Sinal de \(v_i\) é o primeiro sinal encontrado ao realizar o laço.
Exemplo
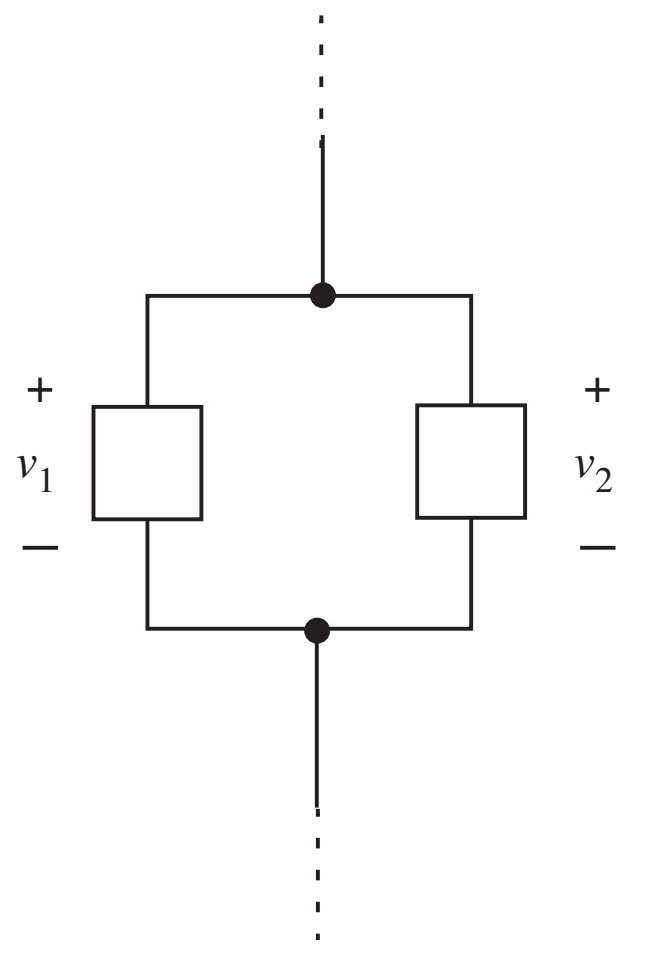
- O que a lei das tensões indica para o laço abaixo? \(v_1-v_2=0\), ou \(v_1=v_2\). Ramos em paralelo estão sujeitos a mesma d.d.p.
Exemplo
- O que a lei das tensões indica para os laços abaixo? 1 equação para cada laço (loop).
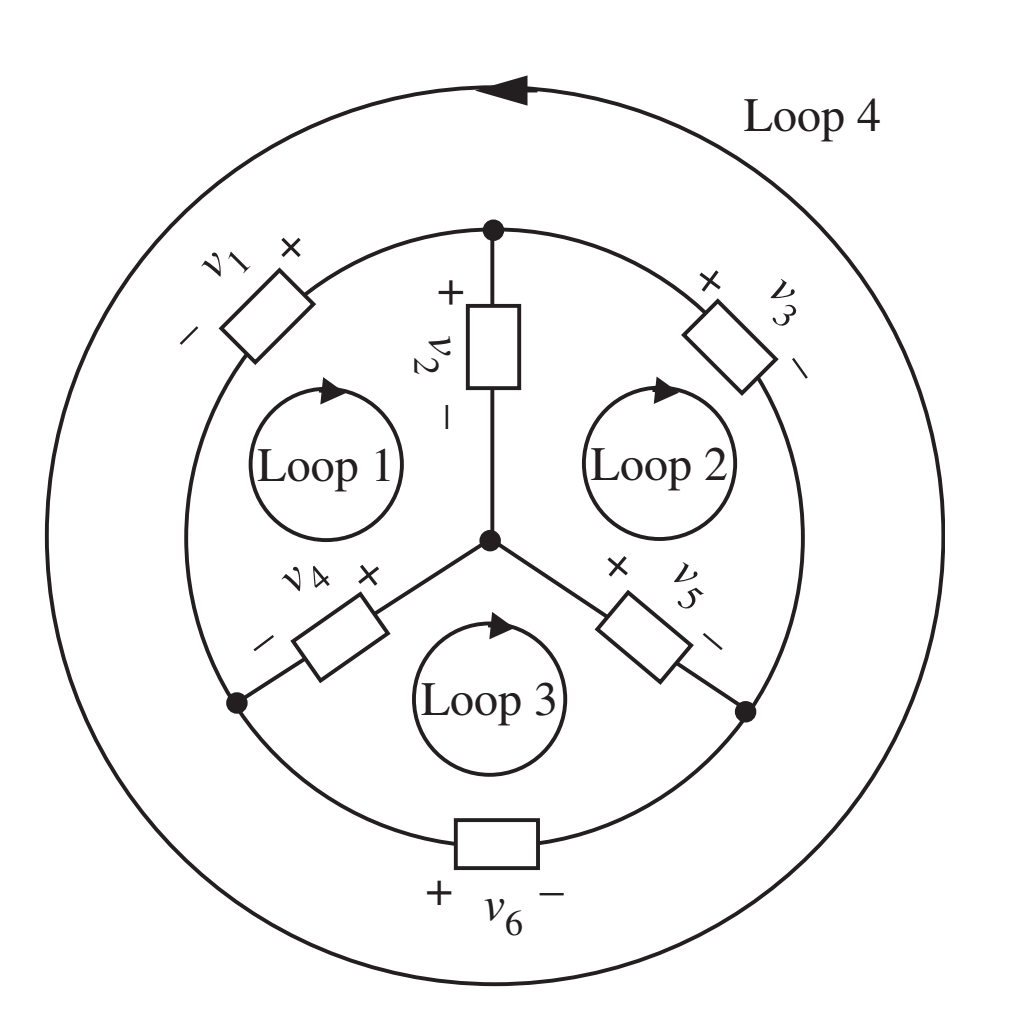
- Nota: Os laços foram escolhidos de forma que a tensão em cada ramo é positiva em um laço e negativa em outro. Com esta definição, a soma das tensões sobre todos os laços é nula.
Exemplo
- Qual o problema com o circuito abaixo? A diferença de potencial entre os terminais em paralelo não é nula e \(\frac{d\Phi_B}{dt} \neq 0\). Você consegue imaginar o que ocorreria numa situação real?

Problema
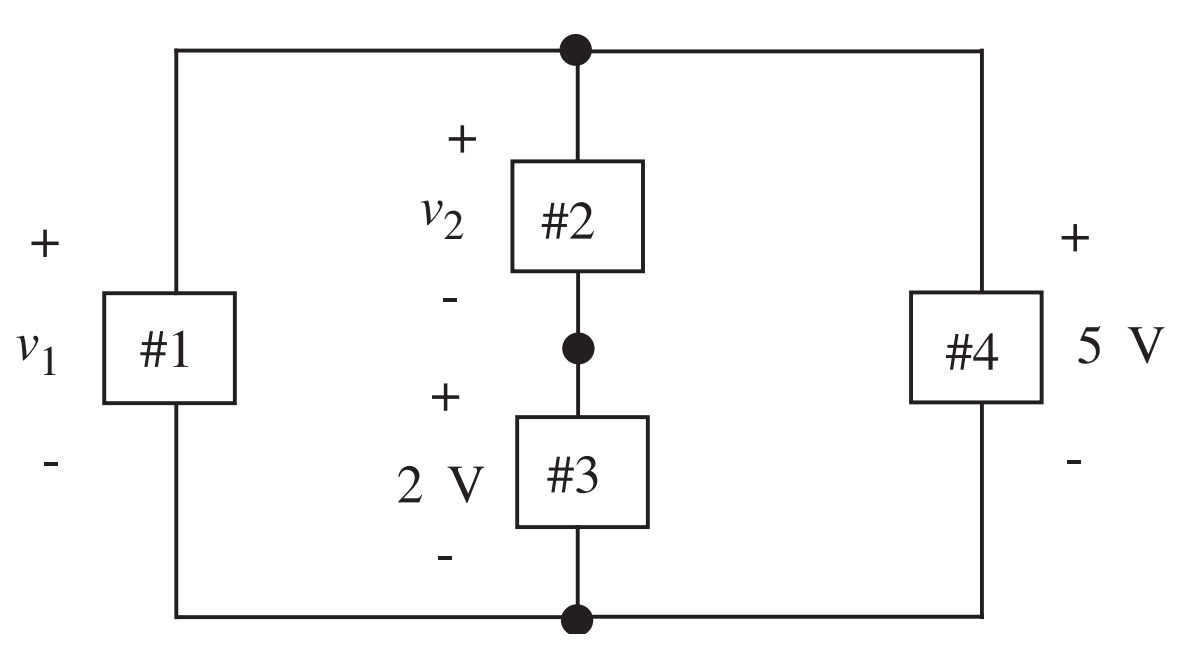
- Determinar os valores de \(v_1\) e \(v_2\) no circuito abaixo. R.: \(v_1=5\text{ V}\) e \(v_2=3\text{ V}\)
Perguntas
- Suponha duas fontes de corrente que fornecem correntes \(i_1\) e \(i_2\) e um resistor de resistência \(r\). Como devemos conectar estas fontes para obter uma corrente \(i=i_1+i_2\) pelo resistor? elementos em paralelo
- Suponha duas fontes de tensão que fornecem tensões \(v_1\) e \(v_2\) e um resistor de resistência \(r\). Como devemos conectar estas fontes para obter uma tensão \(v=v_1+v_2\) entre os terminais do resistor? elementos em série
Análise de circuitos: método básico
- Sabemos (em princípio) o comportamento elétrico individual de cada elemento num circuito.
- As leis de Kirchhoff permitem relacionar as tensões e correntes sobre cada elemento.
- Procedimento de aplicabilidade geral:
- Definir as correntes e tensões em cada ramo de forma consistente. Ex.: usando a convenção de variáveis associadas.
- Considerar as relações constitutivas entre tensão e corrente em cada elemento. Ex.: \(v=ri\)
- Aplicar leis de corrente e tensão de Kirchhoff
- Resolver o sistema de equações resultante
Circuitos com um único resistor
- Começaremos com um caso bastante simples. Um circuito com apenas 1 resistor.
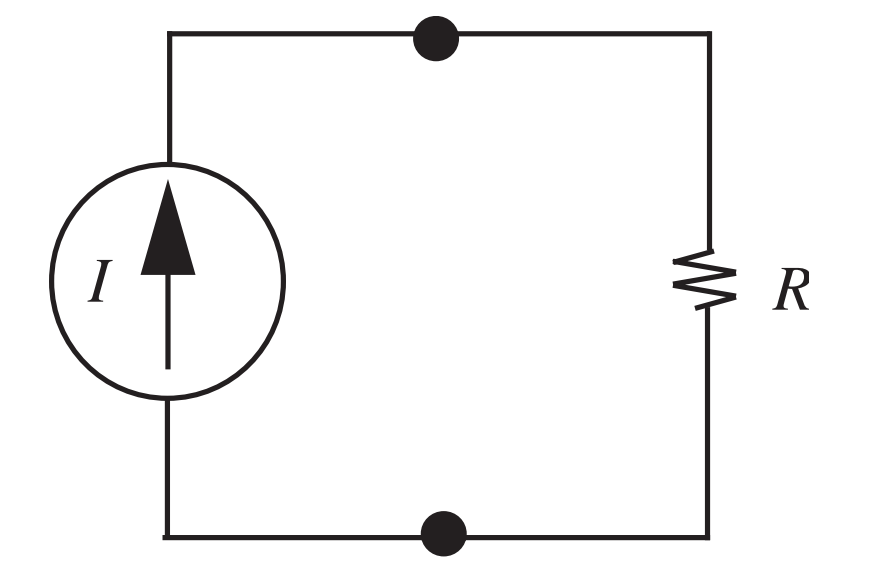
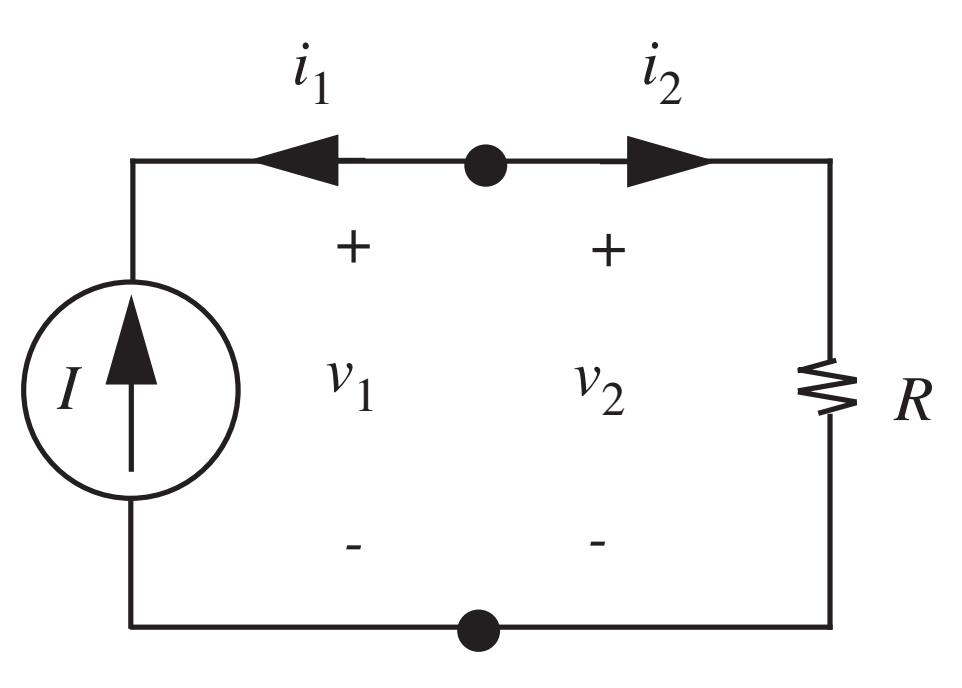
- Definir correntes e tensões
- Relações constitutivas
- \(i_1 = -I\), \(v_2 = R i_2\).
- Leis de Kirchhoff
- Correntes: \(i_1+i_2=0\)
- Tensões: \(-v_1+v_2=0\)
- 4 variáveis de ramo (\(i_1, i_2, v_1, v_2\)) e 4 equações. Resolver o sistema.
- R.: \(-i_1=i_2=I\), \(v_1=v_2=RI\)
- O que acontece se invertermos as definições dos ramos?
Circuitos com um único resistor
- Começaremos com um caso bastante simples. Um circuito com apenas 1 resistor.
- Definir correntes e tensões
- Relações constitutivas
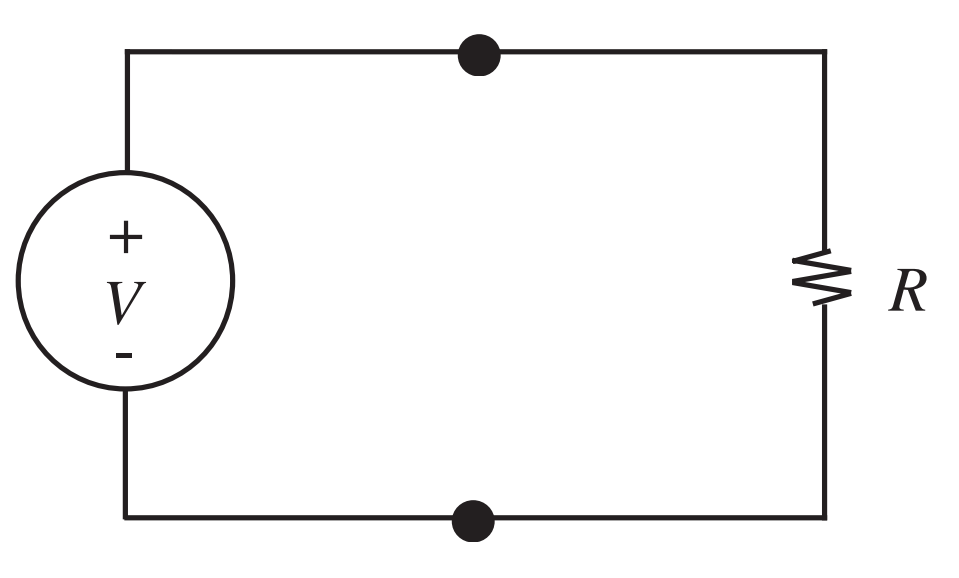
- \(v_1 = V\), \(v_2 = R i_2\).
- Leis de Kirchhoff
- Correntes: \(i_1+i_2=0\)
- Tensões: \(-v_1+v_2=0\)
- 4 variáveis de ramo (\(i_1, i_2, v_1, v_2\)) e 4 equações. Resolver o sistema.
- R.: \(v_1=v_2=V\), \(-i_1=i_2=V/R\)
Conservação de energia
- Uma vez determinadas as variáveis de ramo do circuito, pode-se determinar como a energia está fluindo no circuito.
- Potência no elemento \(j\): \(P_j=v_j i_j\)
- R.: \(-i_1=i_2=I\), \(v_1=v_2=RI\)
- \(i_1 v_1 = -RI^2\)
- \(i_2 v_2 = RI^2\)
- A potência dissipada no resistor é gerada na fonte de corrente.
- Cons. Energia: a energia fornecida pelas fontes é dissipada por um dado conjunto de elementos.
- Útil na verificação de resultados
Exemplo
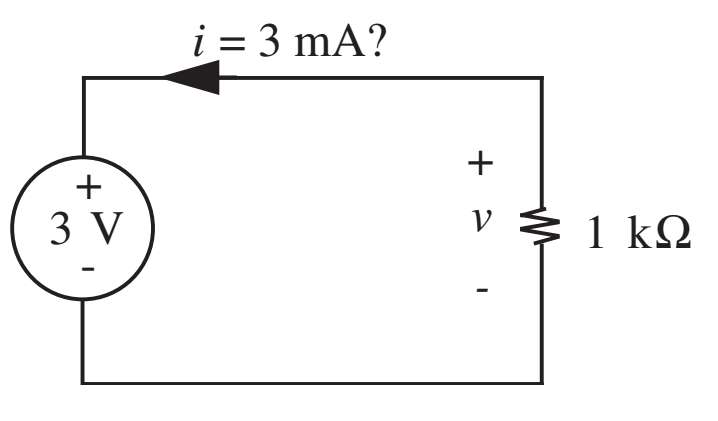
- O circuito abaixo satisfaz a conservação de energia?
- Não, pois o sentido da corrente especificado indica que existe energia entrando na fonte de tensão. \(P_{resistor} = i^2 R = 9\text{ mW}\), \(P_{fonte} = 3\text{ V}\times 3{ mA} = 9\text{ mW}\).
Pergunta
- Suponham que queremos estudar um circuito mais complicado, contendo 2 resistores. De quantas formas podemos conectar os 2 resistores?
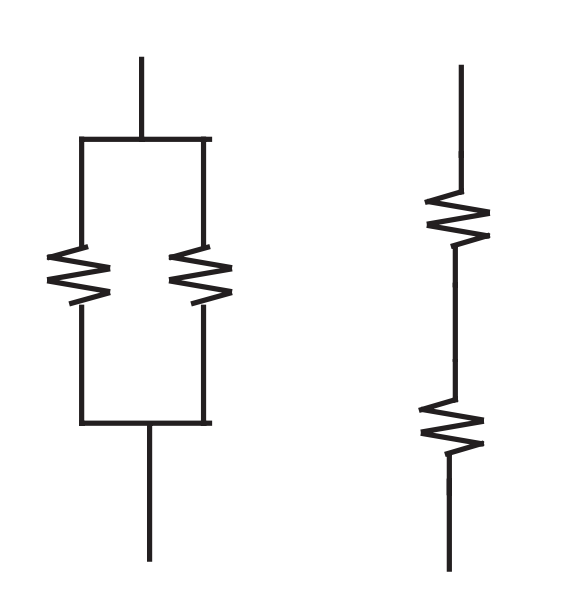
![]()
- Existem 2 topologias possíveis
Divisor de tensão
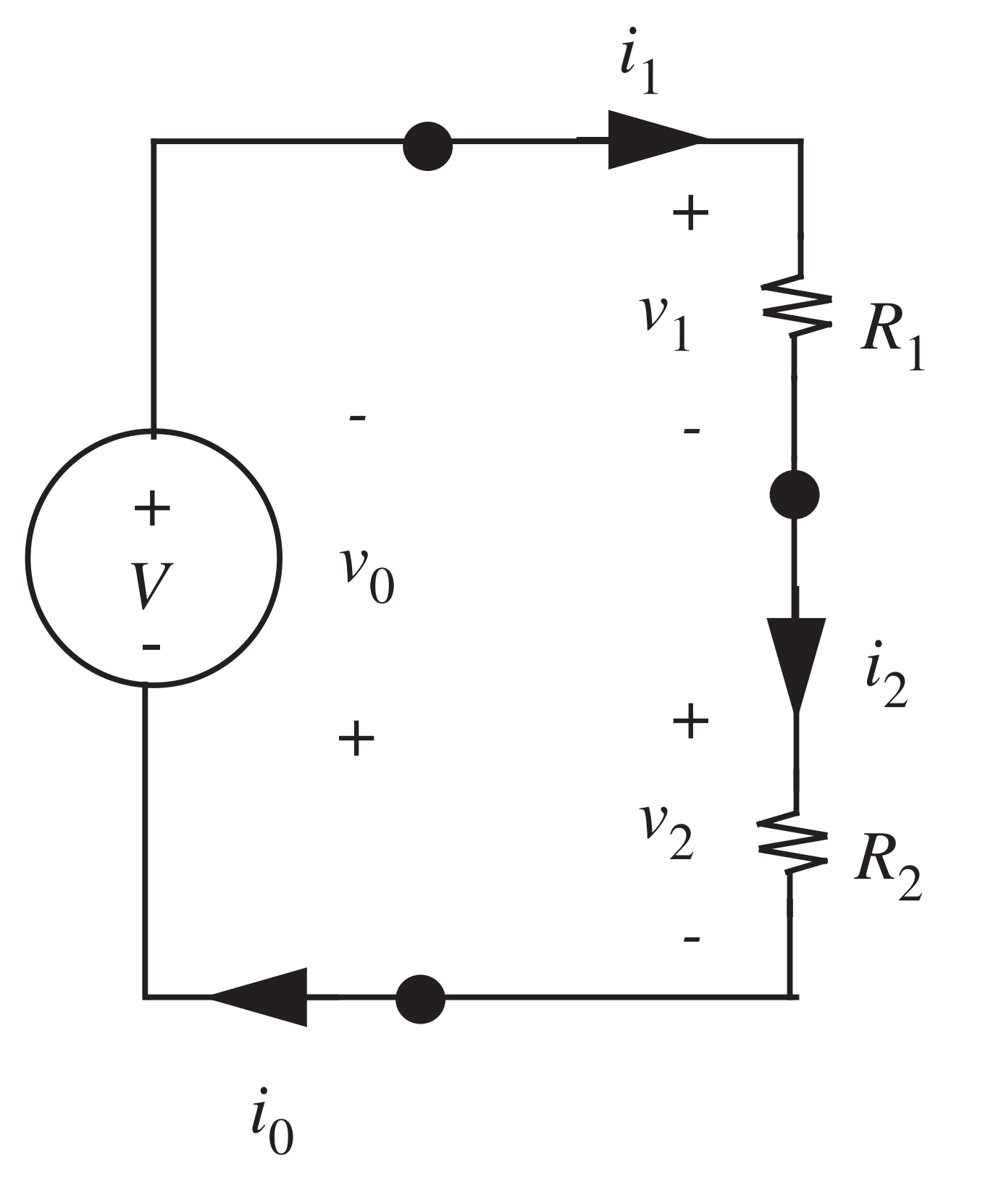
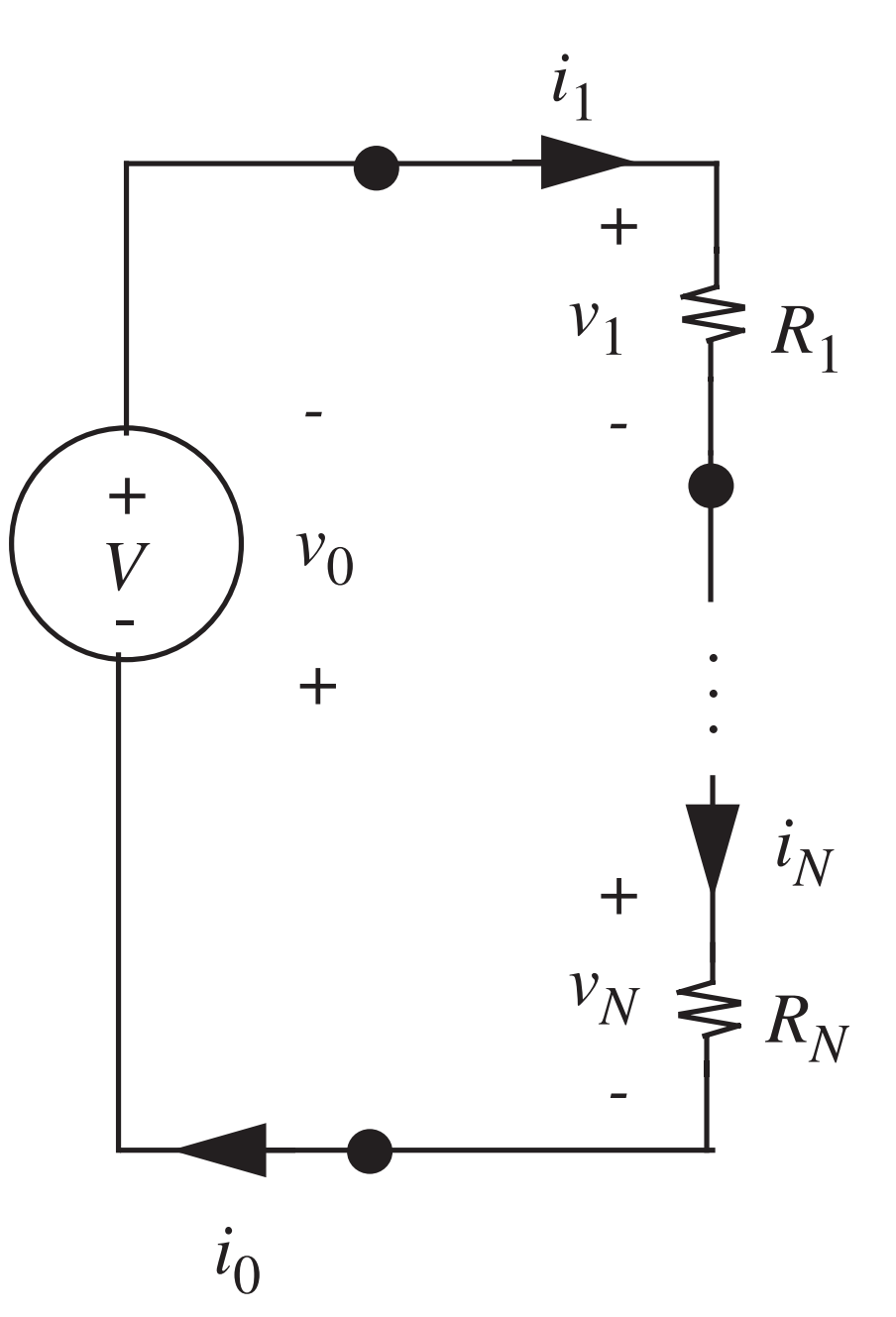
- Um dos tipos de circuitos mais recorrentes é o divisor de tensão
- Temos \(v_0=-V\), \(v_1=R_1i_1\) e \(v_2=R_2i_2\)
- Kirchhoff:
- Correntes: \(i_0=i_1\), e \(i_1=i_2\)
- Tensões: \(v_0+v_1+v_2=0\)
- Sol.: \[i_0=i_1=i_2=\frac{1}{R_1+R_2} V,\] e \[v_1=\frac{R_1}{R_1+R_2} V,\] \[v_2=\frac{R_2}{R_1+R_2} V\]
- Note que \(v_2\) é uma fração de \(V\)
Resistores em série
- Quando diversos resistores estão conectados em série, podemos simplificar a descrição do circuito por meio do conceito de resistência equivalentes \(R_{eq}\)
- \(R_{eq}\) equivale a substituição de um conjunto de resistores de um dado ramo
- Quando diversos resistores estão em série, por eles passa a mesma corrente \(i\)
- Para 2 resistores, \(i=\frac{1}{R_1+R_2} V\)
- \(R_{eq} = R_1 + R_2\)
- Para \(N\) resistores, \(R_{eq} = \sum_{j=1}^N R_j\)
Divisor de corrente
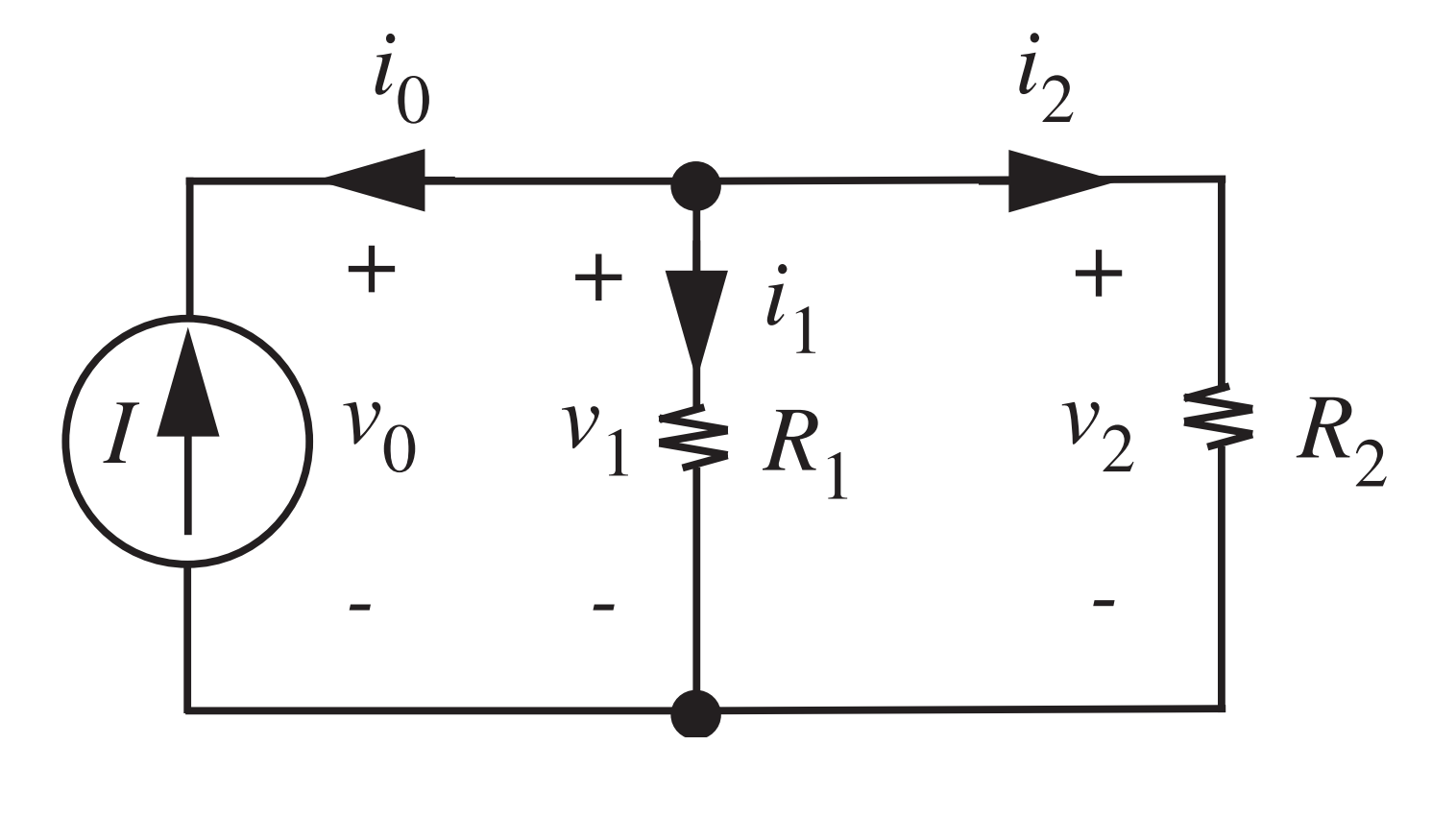
- Circuito análogo ao divisor de tensão, porém para correntes
- Temos \(i_0=-I\), \(v_1=R_1i_1\) e \(v_2=R_2i_2\)
- Kirchhoff:
- Correntes: \(i_0+i_1+i_2=0\)
- Tensões: \(v_0=v_1\), e \(v_1=v_2\)
- Sol.: \[v_0=v_1=v_2=\frac{R_1R_2}{R_1+R_2} I,\] e \[i_1=\frac{R_2}{R_1+R_2} I,\] \[i_2=\frac{R_1}{R_1+R_2} I\]
- Note que \(i_2\) é uma fração de \(I\)
Resistores em paralelo
- Quando diversos resistores estão conectados em paralelo, também podemos simplificar a descrição do circuito por meio do conceito de resistência equivalentes \(R_{eq}\)
- Quando diversos resistores estão em paralelo, é aplicada sobre eles a mesma tensão
- Para 2 resistores, \(v=\frac{R_1R_2}{R_1+R_2} I\)
- \(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}\)
- Para \(N\) resistores, \(\frac{1}{R_{eq}} = \sum_{j=1}^N \frac{1}{R_j}\)

Pergunta
- Suponham que queremos estudar um circuito ainda mais complicado, contendo 3 resistores. De quantas formas podemos conectar os 3 resistores?
![]()
- Existem 4 topologias possíveis
- Podemos simplificar estas topologias em termos de um único resistor, verificando as associações em série e paralelo adequadas.
Circuito com 2 fontes independentes
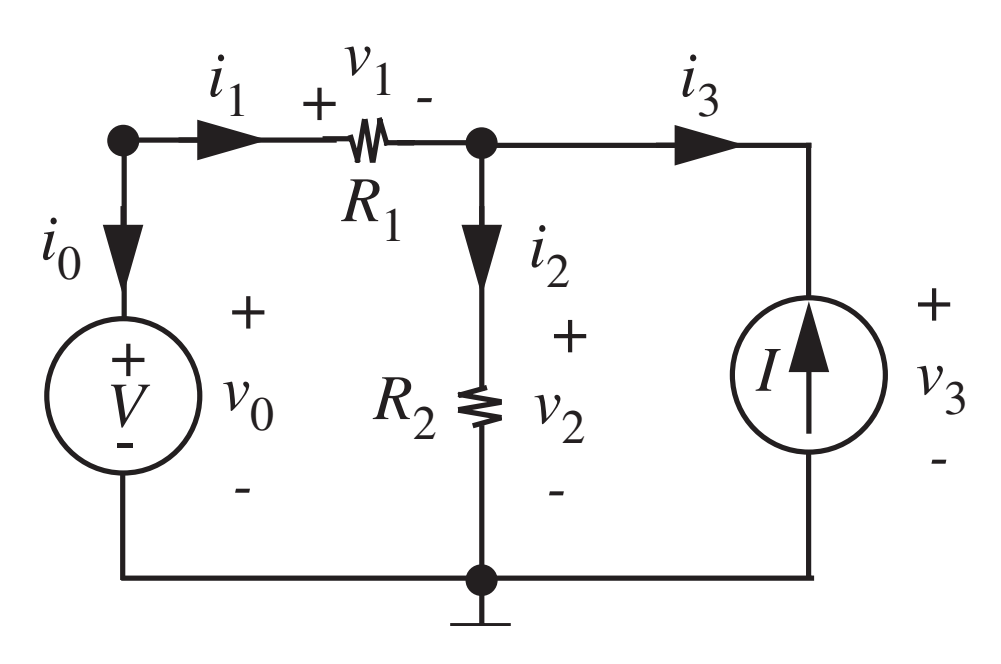
- Até aqui vimos apenas circuitos com 1 fonte apenas. Entretanto, nada impede que tenhamos mais de um tipo de fonte operando em um dado circuito.
- Problema: determinar \(v_2\) em termos de \(V\) e \(I\)
- R.: \(v_2 = \frac{R_1R_2}{R_1+R_2} I + \frac{R_2}{R_1+R_2} V\)
- Notar que a resposta total é uma combinação linear das respostas associadas a \(V\) e \(I\) separadamente.
Análise pelo método de nós
- Vimos anteriormente como analisar circuitos considerando as tensões e correntes por cada elemento.
- Dificuldade: para um circuito com \(N\) elementos, precisamos de \(2N\) variáveis. Exceto para circuitos muito simples e/ou simétricos, este tipo de abordagem é impraticável para um grande número de variáveis.
- Pode-se simplificar consideravelmente a analise do circuito em termos das tensões em cada nó
- Tensão do nó: d.d.p. entre um dado nó e um nó de referência (terra, ou ground)
Análise pelo método de nós
- A corrente flui sempre do nó de maior tensão para o de menor tensão.
- A escolha do nó de referência (terra) é arbitrária. Escolha mais conveniente: nó com maior número de elementos conectados.
- Vantagem importante: Ao invés de lidarmos com tensões e correntes em cada elemento, precisamos apenas definir as tensões nos nós e correntes nos ramos. Lei das tensões é satisfeita automaticamente.
Procedimento de análise
- Para encontrar as variáveis do circuito, pode-se seguir o roteiro abaixo:
- Selecionar um nó de referência (terra), cujo potencial é \(0\) V.
- Rotular os potenciais em relação ao terra em cada outro nó do circuito. Nós conectados ao terra por fontes de tensão possuem a tensão da fonte.
- Escrever a lei das correntes para cada nó em que a tensão é desconhecida. 1 eq. por nó.
- Resolver o sistema de equações encontrado.
- Determinar variáveis de ramo/elemento conforme a necessidade.
Exemplo
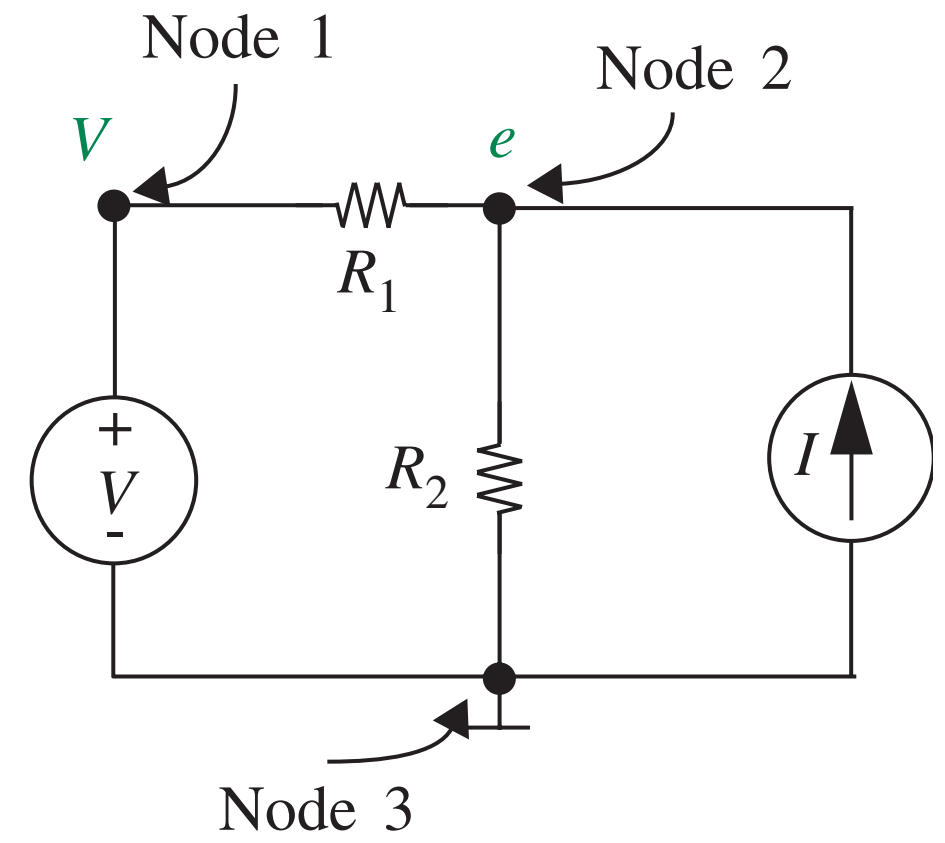
- Voltemos ao circuito anterior com duas fontes
- Problema: determinar \(e\) em termos de \(V\) e \(I\)
- R.: \(e = \frac{R_1R_2}{R_1+R_2} I + \frac{R_2}{R_1+R_2} V\)
- Notar que precisamos de um número menor de etapas para encontrar a resposta.
Exemplo
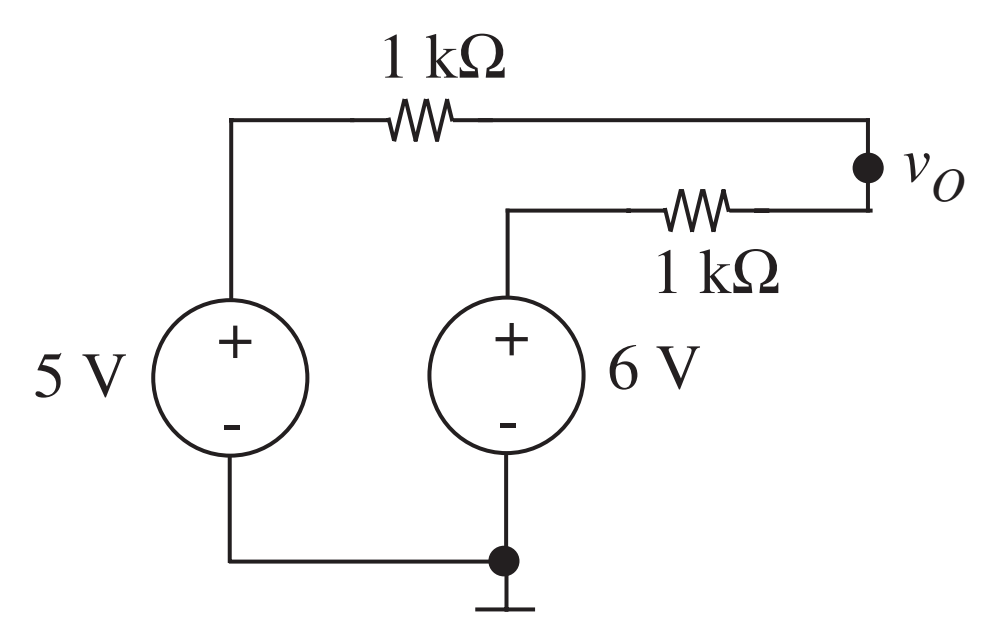
- Qual a tensão no terminal \(v_O\)?
- \(\frac{v_O-5}{1k}+\frac{v_O-6}{1k}=0\)
- \(v_O = \frac{5 + 6}{2}\)
- Circuito somador, com fator de escala \(\frac{1}{2}\).
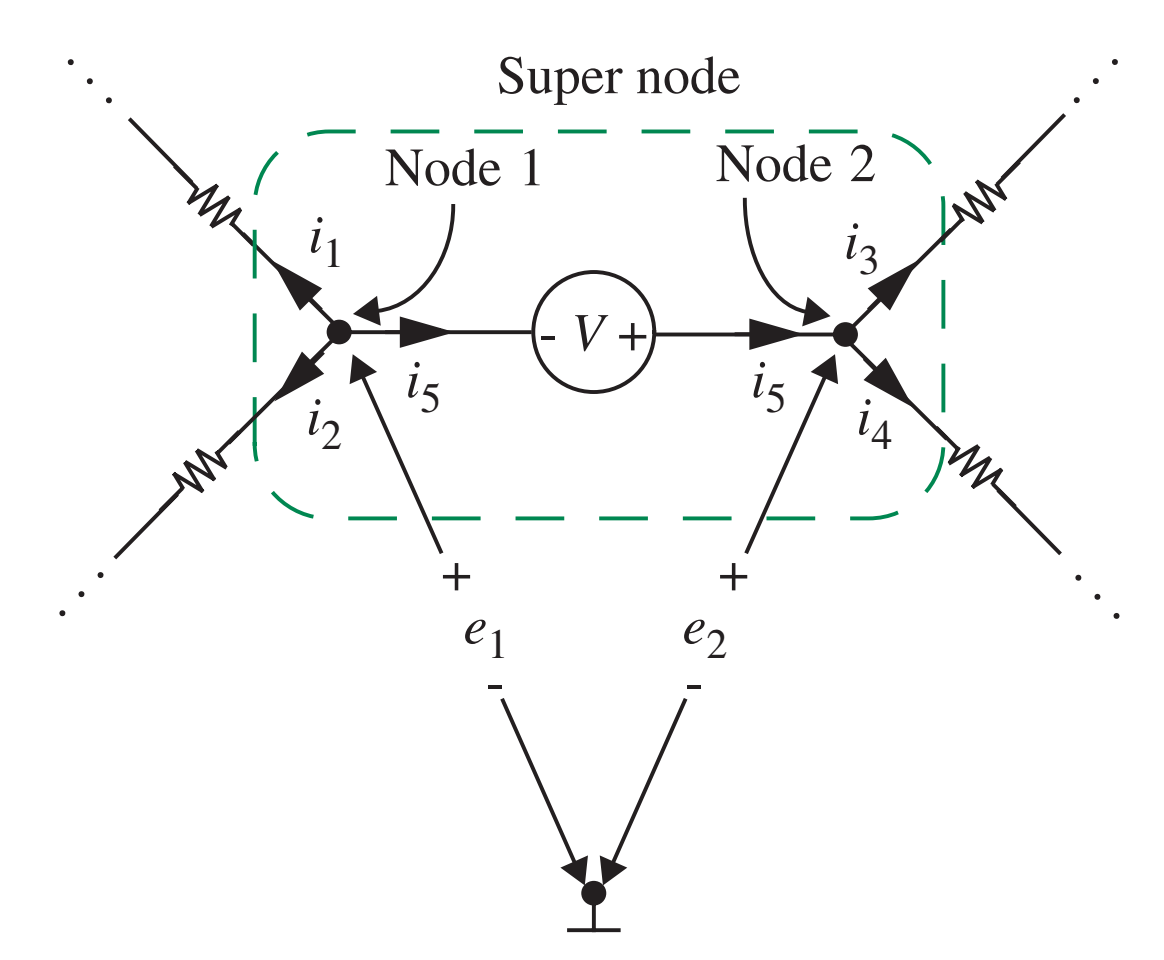
Fonte de tensão flutuante
- Como analisar uma fonte de tensão que não está conectada à referência (terra)?
- Utilizando o conceito de super nó.
- \(e_2 = e_1 + V\)
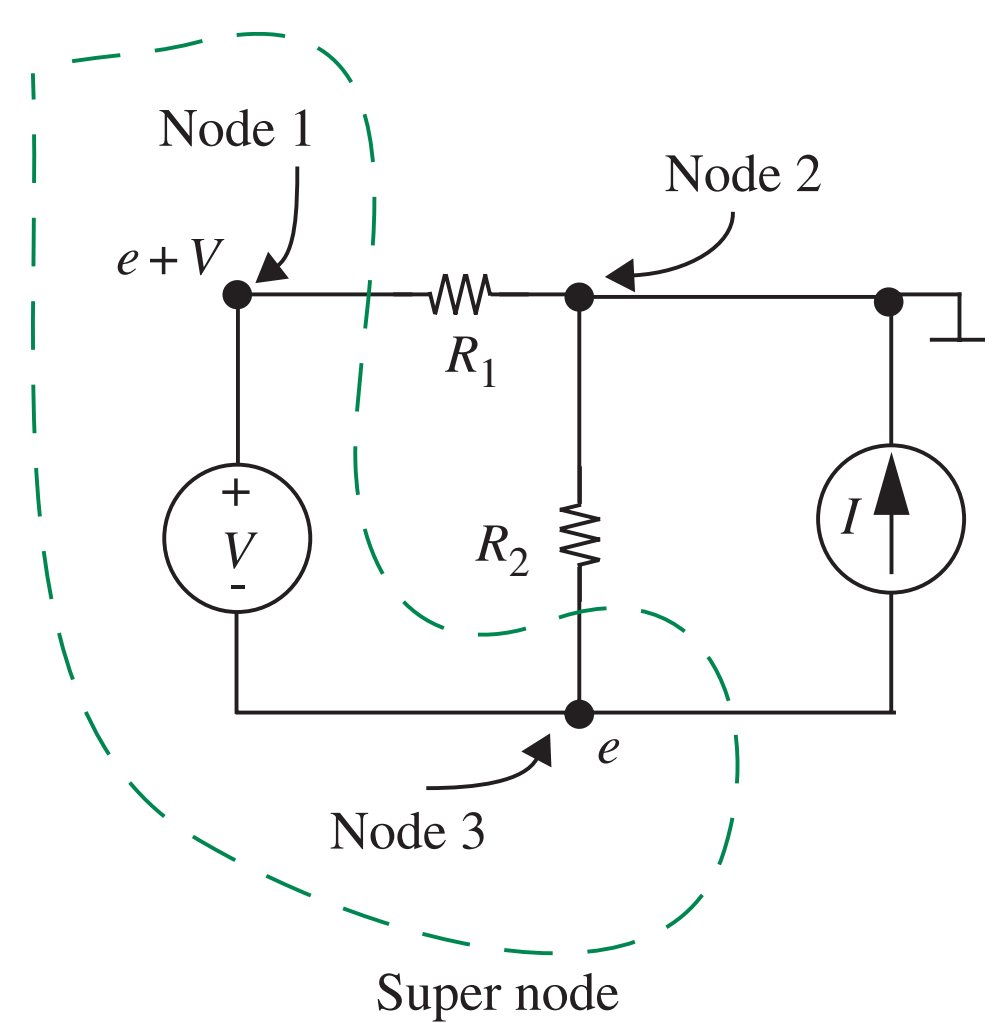
Exemplo
- Qual o valor de \(e\)?
- Podemos determinar as correntes no nó 2, e encontrar…
- \(e=-\frac{R_1R_2}{R_1+R_2} I - \frac{R_2}{R_1+R_2} V\)
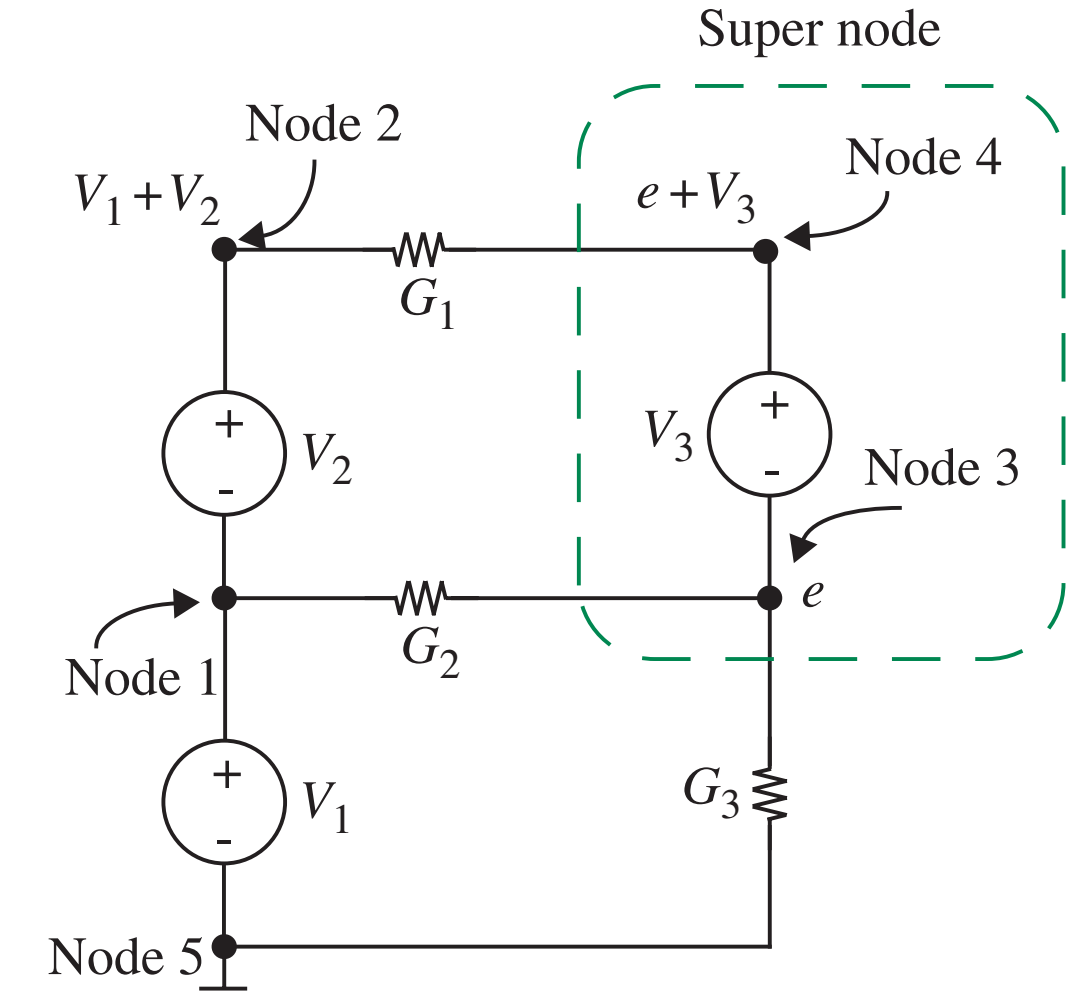
Exemplo
- Qual o valor de \(e\)? Nota: condutância \(G_i=1/R_i\).
- Determinar correntes nos nós 3 e 4…
- \(e=\frac{G_1(V_1+V_2-V_3)+G_2V_3}{G_1+G_2+G_3}\)
Linearidade e superposição
- Perceba que as tensões e correntes em cada ponto do circuito (\(v_j,i_j\)) são proporcionais às tensões e correntes das fontes (\(V_j,I_j\)). Resposta linear.
- Não há termos envolvendo produtos entre fontes.
- Ex.: \(e = \frac{R_1R_2}{R_1+R_2} I + \frac{R_2}{R_1+R_2} V\)
- Podemos saber a resposta devido ao conjunto das fontes superpondo as respostas individuais (i.e., “desligando” todas as outras fontes)
- Fontes de tensão “desligadas”: \(0\) V (curto circuito)
- Fontes de corrente “desligadas”: \(0\) A (circuito aberto)
Adicionador resistivo
- Qual a dependência de \(V_0\) em termos de \(V_1\),\(V_2\),…?
- \(V_{0,1} = \frac{R/3}{R+R/3} V_1\)
- \(V_{0} = \frac{1}{4} (V_1+V_2+V_3+V_4)\)
- Princípio da escada R-2R (conversão digital analógica)

Curva característica \(I\times V\)
- Um dispositivo genérico pode ser representado por um circuito equivalente (modelo). \(i\) e \(v\) devem satisfazer alguma relação.
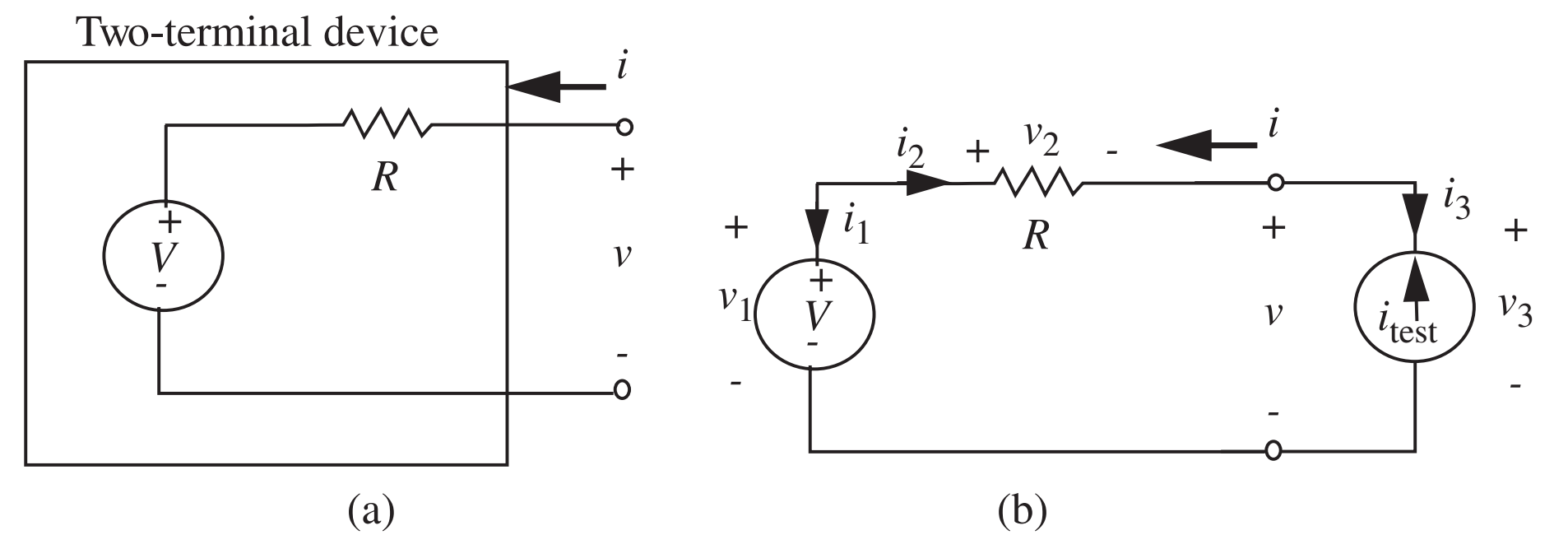
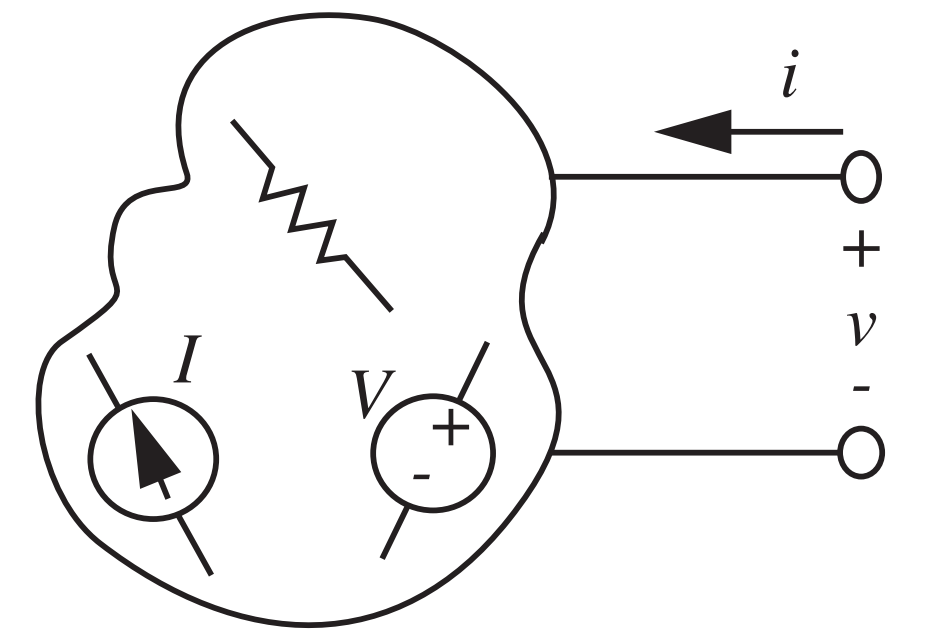
- Consideremos um dispositivo de 2 terminais conforme a figura (a) abaixo. Qual é a relação entre \(i\) e \(v\)?
![]()
- Podemos analisar a resposta do circuito ao conectar uma fonte de tensão e/ou corrente aos terminais externos.
- R.: \(i=\frac{v-V}{R}\)
Curvas características de elementos básicos
- Pergunta: como são as curvas características de corrente vs tensão dos seguintes elementos:
- Fonte de tensão ideal
- Fonte de corrente ideal
- Resistor
- Circuito aberto e curto-circuito
- R.: 1. reta horizontal, 2. reta vertical, 3. reta pela origem e 4. Retas horizontal e vertical passando pela origem.
Pergunta
- Suponha que temos um circuito contendo resistores, e fontes de tensão e corrente conectadas de formas desconhecidas. Ex.: uma bateria ou fonte de tensão real.
- Este circuito possui 2 terminais que são acessíveis externamente. Ex.: terminais da bateria/fonte
- Do que precisamos para encontrar a curva característica \(I\times V\)?
- Se o circuito satisfaz a superposição linear, precisamos apenas de 2 informações!
Equivalente de Thévenin
- Ex.: Bateria
- Analisar a resposta do circuito quando os terminais estão desconectados
- \(v = v_{Th} = v_{OC}\) (tensão de circuito aberto)
- “Desligar” a fonte de tensão interna, e ver a resposta do circuito a uma fonte externa.
- Ex.: se \(i=i_{teste}\), com \(V=0\), teremos uma tensão \(v_a = R_{Th} i_{teste}\) entre os terminais.
- Então, \[v = v_{OC} + R_{Th} i \]
- Curva característica equivalente a uma fonte de tensão em série com uma resistência \(R_{Th}\)

Exemplo
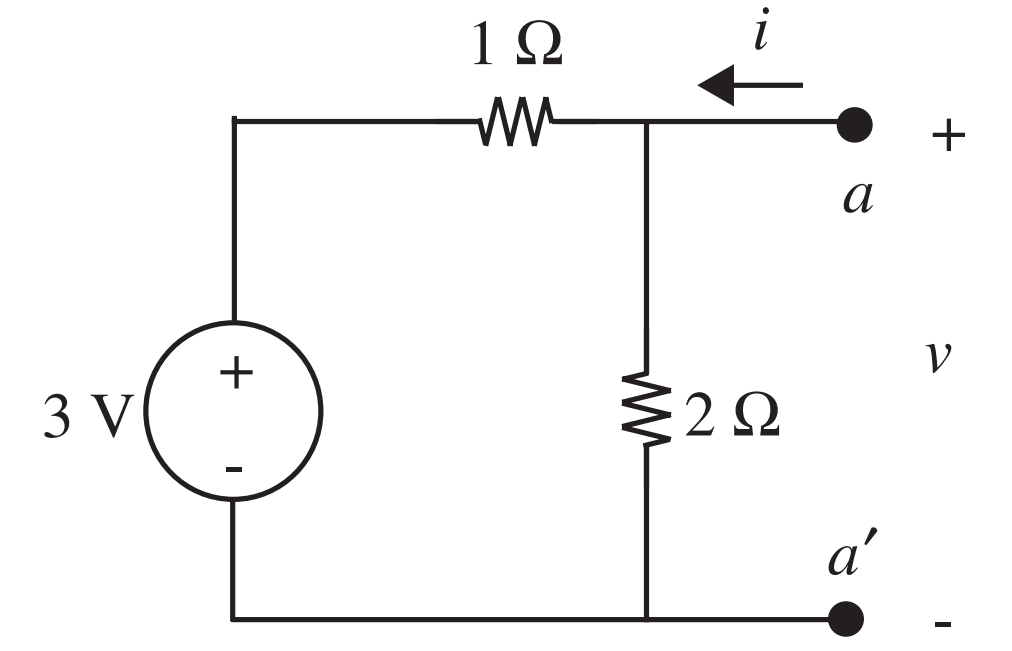
- Encontrar o circuito de Thévenin equivalente ao da figura ao lado, onde os terminais são \(a\) e \(a'\)
- \(v_{Th}=\frac{2}{1+2}3=2\) V
- \(R_{Th}=\frac{1.2}{1+2} = \frac{2}{3}\Omega\)
Exemplo
- Encontrar o circuito de Thévenin equivalente ao da figura ao lado, onde os terminais são \(a\) e \(a'\)
- \(v_{Th}=2.2=4\) V
- \(R_{Th}=2\Omega\)
- Se uma fonte de tensão com \(V=1\) V for conectada entre \(a\) e \(a'\), qual a corrente \(i\) que a atravessa?
- \((v_{Th}-V)=R_{Th} i\), e \(i=\frac{3}{2}\) A
- Circuitos complexos contendo fontes e resistores podem ser simplificados usando equivalentes de Thévenin. Compare esta ultima parte do problema a uma análise direta.
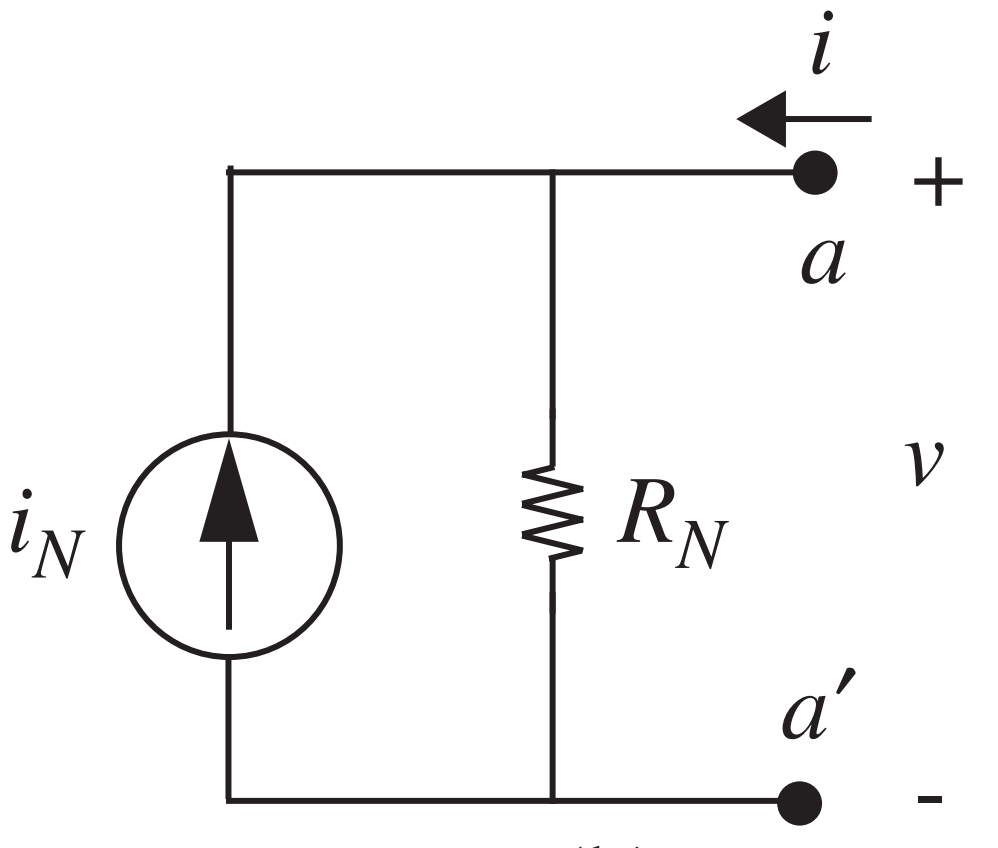
Equivalente de Norton
- Podemos expressar o circuito equivalente também em termos de uma fonte de corrente.
- Análogo ao equivalente de Thévenin
- Considerar a resistência \(R_N\) do circuito com a fonte de corrente “desligada”. (\(R_N=R_{Th}\))
- A corrente \(i_N\) da fonte deve ser tal que a d.d.p. entre os terminais é igual àquela observada quando os terminais estão desconectados
Exemplo
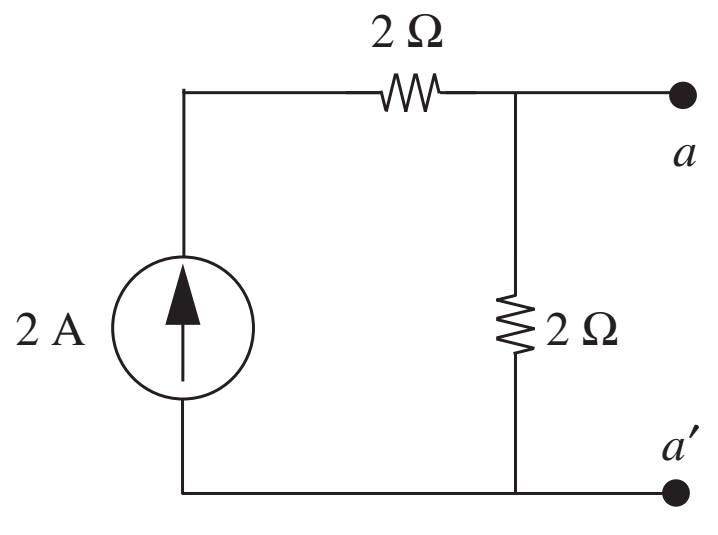
- Encontrar o circuito de Norton equivalente ao da figura ao lado, onde os terminais são \(a\) e \(a'\)
- \(R_N=\frac{1.2}{1+2} = \frac{2}{3}\Omega\)
- \(v_{aa'}=2\) V
- \(i_N= \frac{v_{aa'}}{R_N}=3\) A