Sinais analógicos
FI577 - Instrumentação eletrônica para a física
Leitura recomendada: Horowitz & Hill Cap. 1 e Agarwal Caps. 10 e 13
Resposta transiente: circuito RC
- Até aqui, os sinais considerados eram constantes no tempo
- Agora consideraremos tensões e correntes que variam no tempo
- O primeiro circuito é o circuito RC
![]()
Descrição matemática
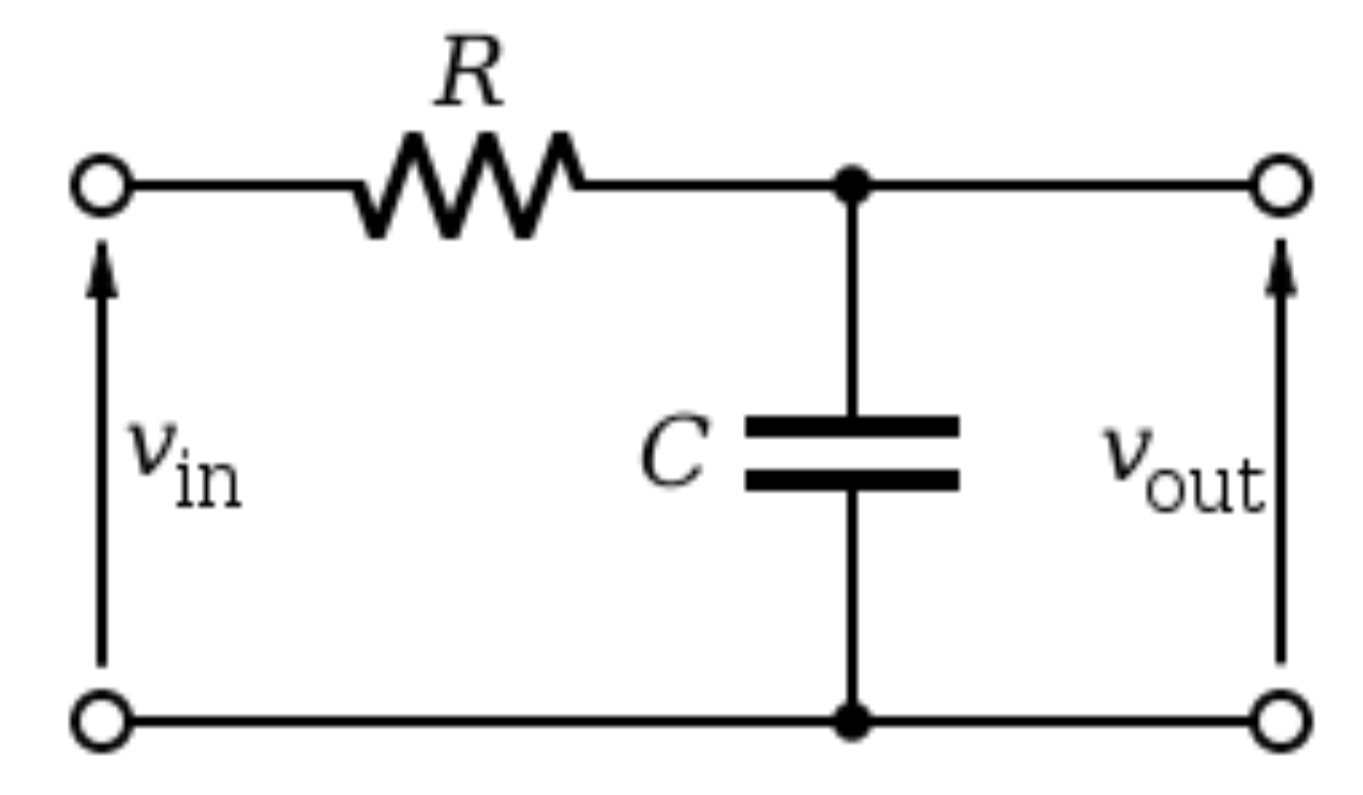
- Tensão aplicada: \(V_S\)
- Tensão no Capacitor: \(q=Cv\)
- Tensão no resistor: \(v_S-v = R i\)
- Problema: Como encontrar \(v\), se \(V_S\) varia no tempo?
Solução: montar uma equação diferencial
- Temos que \(q=Cv\) e \(\frac{v_S-v}{R} = i\)
- Lembrando, \(i\) indica quanta carga flui pelo fio por unidade de tempo (C/s), podemos usar que \(i=\frac{dq}{dt}\)
- Daí, \(q = Cv\), ou \(\frac{dq}{dt} = i = C\frac{dv}{dt}\)
- Então, \(\frac{v_S-v}{R}=C\frac{dv}{dt}\), ou passando \(v\) para um mesmo lado da eq.,
- \[RC\frac{dv}{dt} + v = V_S\]
- Agora só precisamos resolver a equação diferencial
Solução homogênea (\(V_S=0\))
\[RC\frac{dv}{dt} + v = V_S\]
- A solução mais simples para a Eq. Dif. ocorre quanto \(V_S=0\)
- Note então que \(RC\frac{dv}{dt} + v = 0\), ou \(\frac{dv}{dt} =-\frac{1}{RC}v\).
- Que função é proporcional a sua derivada?
- \(v\) é uma função tipo exponencial! Podemos verificar de maneira mais rigorosa, caso façamos a integração
- \(\frac{dv}{v}=-\frac{dt}{RC}\) -> Integrando o tempo de \(0\) a \(t\), temos
- \(\log{\frac{v}{v_0}}=-\frac{t}{RC}\), ou então \(v = v_0 e^{-t/RC}\)
- \(\tau = RC\) é conhecido como o tempo de carga/descarga do capacitor, ou tempo característico do circuito
- Notar que \(\lim_{t\rightarrow\infty} v =0\).
Solução inhomogenea (\(V_S\neq 0\))
\[RC\frac{dv}{dt} + v = V_S\]
- Supor \(v = v_0 e^{-t/RC} + v_1\)
- \(\frac{dv}{dt} = -\frac{v_0}{RC} e^{-t/RC}\)
- \(RC\frac{dv}{dt} + v = -RC\frac{v_0}{RC} e^{-t/RC} + v_0 e^{-t/RC} + v_1 = V_S\)
- \(v_1 = V_S\) é solução
- \(v = v_0 e^{-t/RC} + v_S\)
O que acontece quando \(V_S\) liga abruptamente?
- \(v = v_0 e^{-t/RC} + v_S\) é tal que \(v(0)=0\)
- \(0 = v_0 e^0 + v_S\), ou \(v_0 = - v_S\)
- Finalmente, \[v = V_S \left(1- e^{-t/RC}\right)\]
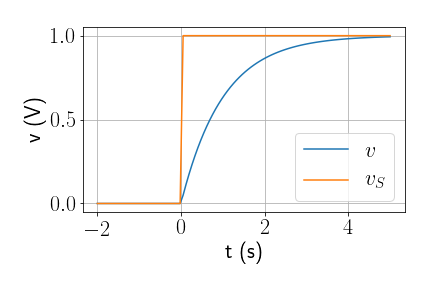
O que acontece quando \(V_S\) desliga abruptamente?
- Supondo que a fonte de tensão \(v_S\) está ligada a muito tempo, e é desligada em \(t=0\), quem são \(v(t=0^-)\) e \(v(t\rightarrow\infty)\)?
- \(v = a e^{-t/RC} + b\) é tal que \(v(0)=v_S\) e \(v(\infty)=0\)
- \(v_S = a + b\), e \(0 = b\)
- Finalmente, \[v = V_S \left(e^{-t/RC}\right)\]

Análise intuitiva
- Podemos analisar o que ocorre com o circuito RC em tempos curtos e longos.
- \(v = a e^{-t/RC} + b\)
- \(t \leq 0\)
- \(v_0 = a + b\)
- \(t \gg RC\)
- \(v_\infty = b\)
- \(v = v_0 e^{-t/RC} + v_\infty (1-e^{-t/RC})\)
Componentes passivos sob sinais senoidais
- Fourier: decomposição em senos e cossenos de sinais periódicos e localizados
- Vamos considerar inicialmente \[ V=A \sin (2\pi f t), \]ou \[ V=A \sin (\omega t),\] onde \(\omega=2\pi f\) é a frequência angular do sinal considerado.
- Tipicamente em eletrônica, \(1\text{ Hz}<f<100\text{ MHz}\)
- Amplitude do sinal \(A\)
Algumas notações para a amplitude
- Amplitude \(A\) em \(V=A \sin (\omega t)\)
- Amplitude pico-a-pico: \(V_{pp}=2A\)
- Amplitude RMS (Root Mean Square)
- \(V_{rms} = \sqrt{\frac{1}{T_2-T_1}\int_{T_1}^{T_2} V(t) dt}\)
- Para um sinal senoidal, \(V_{rms}=\frac{A}{\sqrt{2}}\)
- Depende fortemente das características do sinal
- Definições análogas existem para outras quantidades. Ex.: potência \(P\)
- Qual o valor aproximado de \(x\) em \(P_{pp}=x P_{rms}\)?
- \(x\approx 2,83\)
Decibéis
- Para comparar sinais com amplitudes muito distintas é interessante usar uma escala logarítmica
- Sejam dois sinais de potências \(P_1\) e \(P_2\), \[\text{dB} = 10 \log \frac{P_2}{P_1}\]
- Sejam dois sinais de amplitudes \(A_1\) e \(A_2\), \[\text{dB} = 20 \log \frac{A_2}{A_1}\] (\(P_i\propto A_i^2\))
- O dB também é usado para expressar um valor de sinal absoluto
- 0 dBV (1V rms)
- 0 dBm (1 mW)
Resposta em frequência aproximada
- Havíamos visto que para um capacitor, \(i=C \frac{dv}{dt}\).
- O que ocorre sob uma tensão \(v=A \sin (\omega t)\) senoidal?
- \(i=C\omega A \cos (\omega t)\)
- A menos de uma fase constante (\(90^\circ\)), temos
- \(i=\frac{v}{1/\omega C}\)
- “Resistência” dependente da frequência \(R=1/\omega C\)
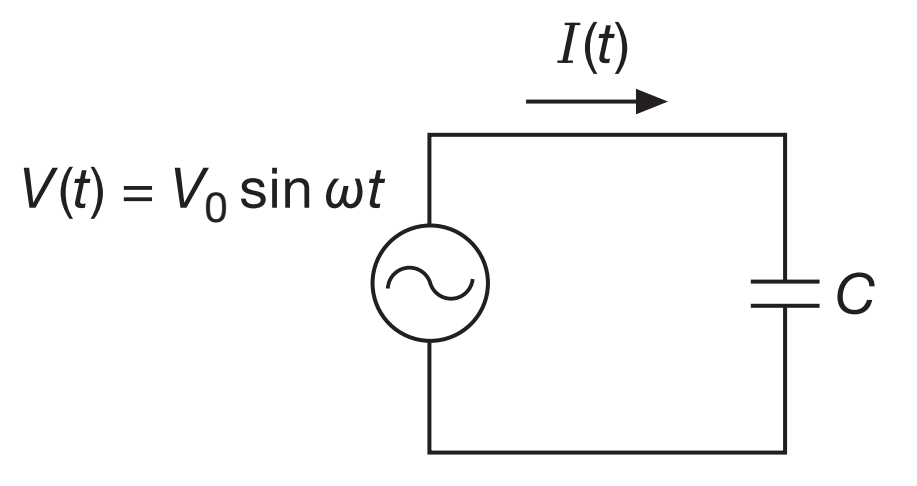
Exemplo
- Filtro RC passa baixa (aproximado)
- Considerar o capacitor como um resistor de resistência \(R=1/\omega C\). \(V_{out}=\)?
- \(V_{out} = V_{in}/(1+\omega R C)\)
- A tensão na saída é pequena se a frequência é grande (\(\omega\gg RC\))
- Como fazer um filtro que permite a passagem de frequências altas usando resistores e capacitores?
- R.: invertendo o capacitor e o resistor
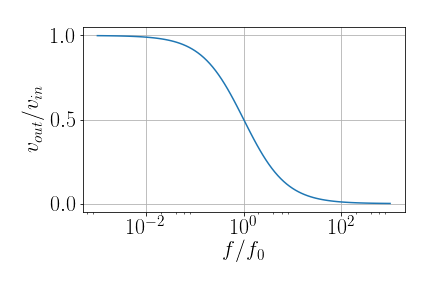

Resposta em frequência completa
- A resposta completa de um dado circuito a um dado sinal senoidal contém variações de amplitude e fase (ex.: \(\cos\omega t = \sin(\omega t - \pi/2)\))
- Problema mais simples se usamos números complexos
- \(v=A \cos (\omega t + \phi) = \mathbb{R}\left\{A e^{j \omega t+\phi}\right\}\)
- Fazemos as operações no domínio dos complexos, e depois consideramos a parte real apenas
Exemplo
- Resposta de um capacitor a uma tensão AC
- \(I=C \frac{dv}{dt}\), com \(v=Ae^{j\omega t}\)
- \(i=j\omega C Ae^{j\omega t} = j\omega C v\)
- Tomando a parte real, \(\mathbb{R}\{v\} = A \cos\omega t\), e \(\mathbb{R}\{i\} = \omega C A \sin\omega t\)
- Podemos ver ainda a lei de Ohm generalizada, \(v = \frac{1}{j \omega C} i = Z i\)
- $Z=(j C)^{-1} $ Impedância do capacitor
Impedância
- A parte imaginária da impedância é denominada de reatância. Capacitores e indutores são elementos reativos.
- Para um indutor de indutância \(L\), a tensão \(V\) e a corrente \(I\) entre seus terminais estão relacionadas por \(V=L\frac{dI}{dt}\).
- Fazendo a mesma análise feita para o capacitor, teremos que \[Z_L=j\omega L\]
- Para cada elemento do circuito, temos \[V = Z I\]
- Como considerar impedâncias em série e em paralelo?
- Usar as regras para associação de resistores!
Exemplo
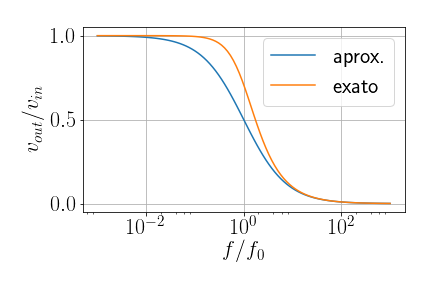
- Filtro RC passa baixa (cálculo completo)
- Considerar um capacitor de impedância \(Z=-j/\omega C\). \(v_{out}=\)?
- \(v_{out} = \frac{-j}{\omega R C-j} v_{in}\)
- \(|v_{out}|=\frac{1}{\sqrt{1+ (\omega R C)^2}} |v_{in}|\)
- Atenuação de 3 dB \([\log(|v_{out}|/|v_{in}|)=\log(1/2)=-3\,\text{dB}]\) em \[f_{3dB}=\frac{1}{2\pi RC}\]
- Qual a fase de \(v_{out}\) em relação a \(v_{in}\)?
- \(\phi = \tan^{-1}(-RC\omega) = -\tan^{-1}\left(\frac{f}{f_{3dB}}\right)\)

Exemplo
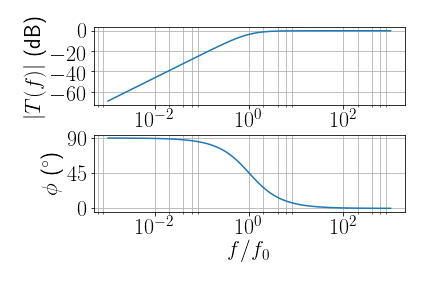
- Filtro RC passa alta
- Considerar um capacitor de impedância \(Z=-j/\omega C\). \(v_{out}=\)?
- \(v_{out} = \frac{R}{R -j (\omega C)^-1} v_{in}\)
- Função de transferência: \(T = \frac{v_{out}}{v_{in}} = \left|T\right|e^{j\phi}\)
- \(|T|=\frac{\omega R C}{\sqrt{1+ (\omega R C)^2}}\)
- \(\phi = \tan^{-1}(\frac{1}{RC\omega}) = -\tan^{-1}\left(\frac{f_{3dB}}{f}\right)\)
- Ponto de 3 dB \([\log(|T|)=\log(1/2)=-3\,\text{dB}]\) em \(f_{3dB}=\frac{1}{2\pi RC}\)

Função de transferência
- Suponha um circuito de 4 terminais, conforme a figura ao lado
- Suponha ainda que \(T\) contém apenas elementos lineares (resistores, capacitores e indutores)
- Pode-se escrever em geral que \(V_O(\omega) = T(\omega) V_I(\omega)\), ou \[T(\omega) = \frac{V_O(\omega)}{ V_I(\omega)}\]
- \(T\) indica como a amplitude e a fase do sinal variam em função da frequência, para todas as frequências
- Conhecendo \(T\) sabemos o comportamento geral do circuito
- Como medir \(T\)? Uma forma possível é introduzir em \(V_O\) um sinal senoidal de frequência conhecida, e medir a amplitude e fase de \(V_I\)
Thévenin generalizado
- Uma consequência importante é o teorema de Thévenin generalizado.
- Uma fonte de sinal que contém apenas elementos lineares pode ser representado por uma fonte de tensão \(V\) (que pode variar no tempo) em série com uma impedância \(Z\)
Breve referência
| Lei elementar | Impedância (\(Z\)) | Admitância (\(Y=1/Z\)) | |
|---|---|---|---|
| Resistor | \(V = R I\) | \(Z_R=R\) | \(Y_R=1/R\) |
| Capacitor | \(C\frac{dV}{dt} = I\) | \(Z_C=-j/(\omega C)\) | \(Y_C=j \omega C\) |
| Indutor | \(V=L\frac{dI}{dt}\) | \(Z_L=j \omega L\) | \(Y_L=-j/(\omega L)\) |
Onde assume-se que as tensões e correntes possuem uma dependência temporal \(V=Ae^{j\omega t}\)