Filtros passivos
FI577 - Instrumentação eletrônica para a física
Leituras recomendadas: Horowitz & Hill Cap. 1 e Agarwal Caps. 10 e 13
Sinais AC e impedância
- Representamos a tensão em termos de números complexos
- \(v=A \cos (\omega t + \phi) = \mathbb{R}\left\{A e^{j \omega t+\phi}\right\}\)
- Fazemos as operações no domínio dos complexos, e depois consideramos a parte real apenas
- Sabendo a relação entre \(v\) e \(i\) para cada elemento linear (resistor, capacitor e indutor), podemos encontrar uma relação tipo \(v=Zi\), onde \(Z\) é chamada de impedância
Exemplo
- Resposta de um capacitor a uma tensão AC
- \(I=C \frac{dv}{dt}\), com \(v=Ae^{j\omega t}\)
- \(i=j\omega C Ae^{j\omega t} = j\omega C v\)
- \(v = \frac{1}{j \omega C} i = Z i\)
- $Z=(j C)^{-1} $ Impedância do capacitor
Breve referência
último slide do capítulo 6
| Lei elementar | Impedância (\(Z\)) | Admitância (\(Y=1/Z\)) | |
|---|---|---|---|
| Resistor | \(V = R I\) | \(Z_R=R\) | \(Y_R=1/R\) |
| Capacitor | \(C\frac{dV}{dt} = I\) | \(Z_C=-j/(\omega C)\) | \(Y_C=j \omega C\) |
| Indutor | \(V=L\frac{dI}{dt}\) | \(Z_L=j \omega L\) | \(Y_L=-j/(\omega L)\) |
Onde assume-se que as tensões e correntes possuem uma dependência temporal \(V=Ae^{j\omega t}\)
Impedância efetiva e função de transferência
- Para cada elemento do circuito, temos \[V = Z I\]
- Como considerar impedâncias em série e em paralelo?
- Usar as regras para associação de resistores!
- Notar que em geral, \(Z=Z(\omega)\) é uma função da frequência.
- Anteriormente encontramos relações entre as tensões em diferentes pontos num circuito
- Ex.: Divisor de tensão: \(V_{out} = \frac{R_2}{R_1+R_2} V_{in} = T V_{in}\)
- \(T \rightarrow\) função de transferência.
- Em circuitos contendo capacitores e indutores, \(T=T(\omega)\)
Exemplo
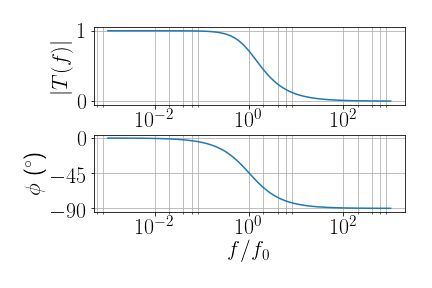
- Filtro RC passa baixa
- Impedâncias \(Z_C=-j/\omega C\) e \(Z_R=R\). \(v_{out}=\)?
- \(v_{out} = \frac{-j}{\omega R C-j} v_{in}\)
- \(T = \frac{-j}{\omega R C-j} = |T|e^{j\phi}\)
- \(|T|=\frac{1}{\sqrt{1+(\omega R C)^2}}\)
- \(\phi = \tan^{-1}(-RC\omega) = -\tan^{-1}\left(\frac{f}{f_{3dB}}\right)\)
- Em \(f_{3dB}=\frac{1}{2\pi RC}\), \(|T|=1/\sqrt{2}\)
Exemplo
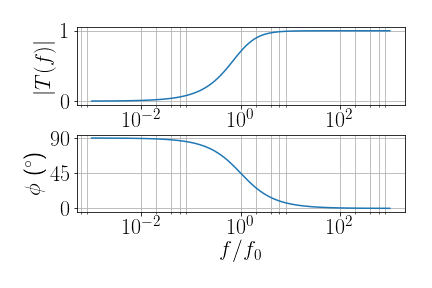
- Filtro RL passa alta
- Impedância do indutor \(Z=j\omega L\). Como devemos conectar \(R\), \(L\) aos terminais?
- \(T = \frac{j L \omega}{R +j L \omega} v_{in}\)
- \(|T|=\frac{\omega L/R}{\sqrt{1+ (\omega L/R)^2}}\)
- Ponto de 3 dB? em \(f_{3dB}=\frac{1}{2\pi}\frac{R}{L}\)
- \(\phi = \tan^{-1}(R/L\omega)\)
- Podemos também obter um passa-baixa invertendo \(R\) e \(L\) no circuito
Circuitos \(LC\)
- Sabemos os efeitos das combinações entre resistores e vimos \(RC\) e \(RL\) em série.
- Formam filtros passa-baixa e passa-alta
- E um circuito sem dissipação, contendo apenas reatância (\(Z\) imaginário)?
- Ex.: \(L\) e \(C\) em paralelo (\(Z_{C} = -j/\omega C\), \(Z_{L} = j \omega L\))
- \(Z_{LC,\text{paralelo}}=\) \(\frac{Z_CZ_L}{Z_C+Z_L} = \frac{L/C}{j(\omega L - 1/\omega C)} = \frac{-j \omega L}{\omega^2LC-1}\)
- Qual a “cara” de \(Z_{LC}\) em função da frequência?
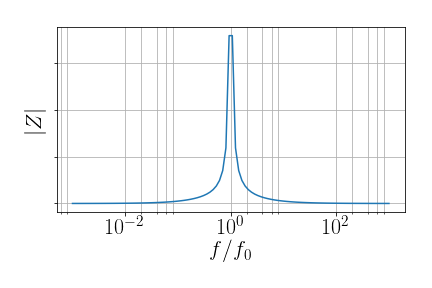
- Se montarmos um divisor de tensão com um resistor em série com LC, o que esperamos para a tensão dividida em \(f=f_0=(LC)^{-1/2}\)?
- E \(f\) longe de \(f_0\)?
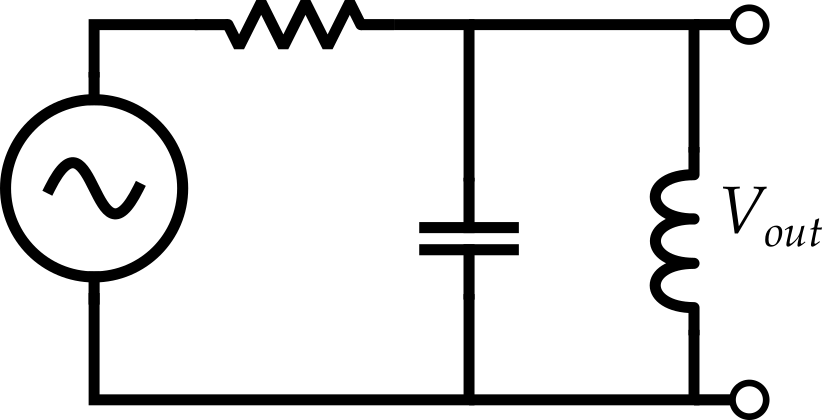
Ressonador RLC
- Colocando um resistor em série com o LC anterior, temos
- \(T(\omega)=\frac{\frac{-j \omega L}{\omega^2LC-1}}{R-j\frac{ \omega L}{\omega^2LC-1}}=\frac{-j \omega L/R}{(\omega^2LC-1)-j\omega L/R}\)
- Definindo \(\omega^2LC=(\frac{\omega}{\omega_0})^2\), \[\omega_0=\frac{1}{\sqrt{LC}}\]
- \(\omega_0\): Frequência de ressonância (onde \(Z_{LC}\rightarrow\infty\))
- Seja \(\omega L/R = \frac{\omega}{\omega_0} \omega_0 L/R = \frac{\omega}{\omega_0} Q\), então \[Q=\frac{1}{R}\sqrt{\frac{L}{C}}\]
- \(Q\): Fator de qualidade (indica a largura da ressonância)
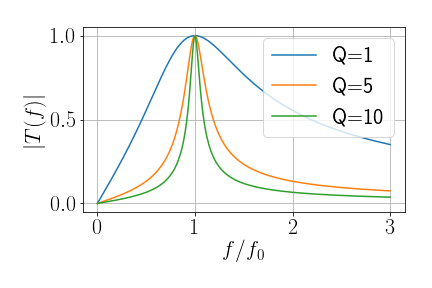
Ressonador RLC
- Qual é a variação da fase?
- \(\phi = \tan^{-1}\left(Q \frac{1-\omega^2/\omega_0^2}{\omega/\omega_0}\right)\)
![]()
- Na ressonância (\(f=f_0\)), a saída está em fase com a entrada (sinais “caminham” juntos)
- Ou seja, apenas um sinal ressonante passa por este circuito (\(Q\gg1\)). Além disto, quando este sinal passa pelo circuito ele mantém sua fase original.
- Filtro passa-banda, com uma largura determinada pelo fator de qualidade \(Q\)
\(LC\) em série
- \(Z_{C} = -j/\omega C\), \(Z_{L} = j \omega L\)
- \(Z_{LC,\text{série}}=\) \(Z_C+Z_L=j \left(\omega L-\frac{1}{\omega C}\right)\)
- Qual a “cara” de \(Z_{LC}\) em função da frequência?
- \(Z_{LC,\text{série}}(\omega\rightarrow 0)=\infty\) e \(Z_{LC,\text{série}}(\omega\rightarrow \infty)=\infty\)
- Se montarmos um divisor de tensão com um resistor em série com LC, o que esperamos para a tensão dividida em \(f=f_0=(LC)^{-1/2}\)?
- E \(f\) longe de \(f_0\)?
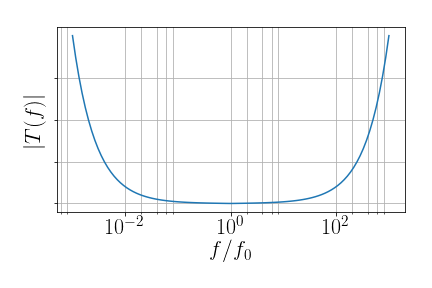
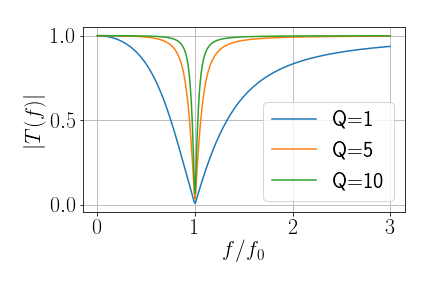
RLC em série
- Colocando um resistor em série com o LC anterior, temos
- \(T(\omega)=\frac{\frac{j}{\omega C}(\omega^2LC-1)}{R+\frac{j}{\omega C}(\omega^2LC-1)}= \frac{j(\omega^2LC-1)}{RC\omega+j(\omega^2LC-1)}\)
- Usando \(\omega_0=\frac{1}{\sqrt{LC}}\), e \(Q=\frac{1}{R}\sqrt{\frac{L}{C}}\),
- \(T = \frac{j((\frac{\omega}{\omega_0})^2-1)}{Q\frac{\omega}{\omega_0}+j((\frac{\omega}{\omega_0})^2-1)}\)
- Este filtro impede a passagem de sinais na frequência de ressonância \(\omega_0\) (Filtro Notch)

Cálculo analógico com um circuito RC
- Suponha um sinal periódico: \(v=Ae^{j\omega t}\)
- \(\frac{dv}{dt} = j\omega v\), enquanto \(\int v dt = \frac{v}{j\omega} + C\)
- Seja \(T = j\omega A\), onde \(A=\text{cte}\)
- Então \(v_{out}=j\omega A v_{in} = A\frac{dv_{in}}{dt}\)
- \(v_{out}\) é a derivada de \(v_{in}\)
- Seja \(T = A/j\omega\), onde \(A=\text{cte}\)
- Então, \(v_{out}= A v_{in}/j\omega = A \int v dt\)
- Podemos calcular usando elementos lineares!
- Basta montar um circuito com a função de transferência correta
- Exemplos na prática 3
Anúncio
Por que usar filtros
- Processamento do sinal de interesse, como eliminação de ruído
- E o que é ruído?
- Tensões e/ou correntes que estão presentes no sistema mas não carregam informação de interesse
- Consultar Horowitz & Hill Cap. 8, ou Application Note (A.N.) SRS - Signal Enhancement.
- Ruído Johnson (excitações térmicas) em um resistor \(R\): \[v_{RMS} = \sqrt{4 k T R \Delta f}\]
- Shot-noise (Flutuações na corrente devido a discretização da carga)
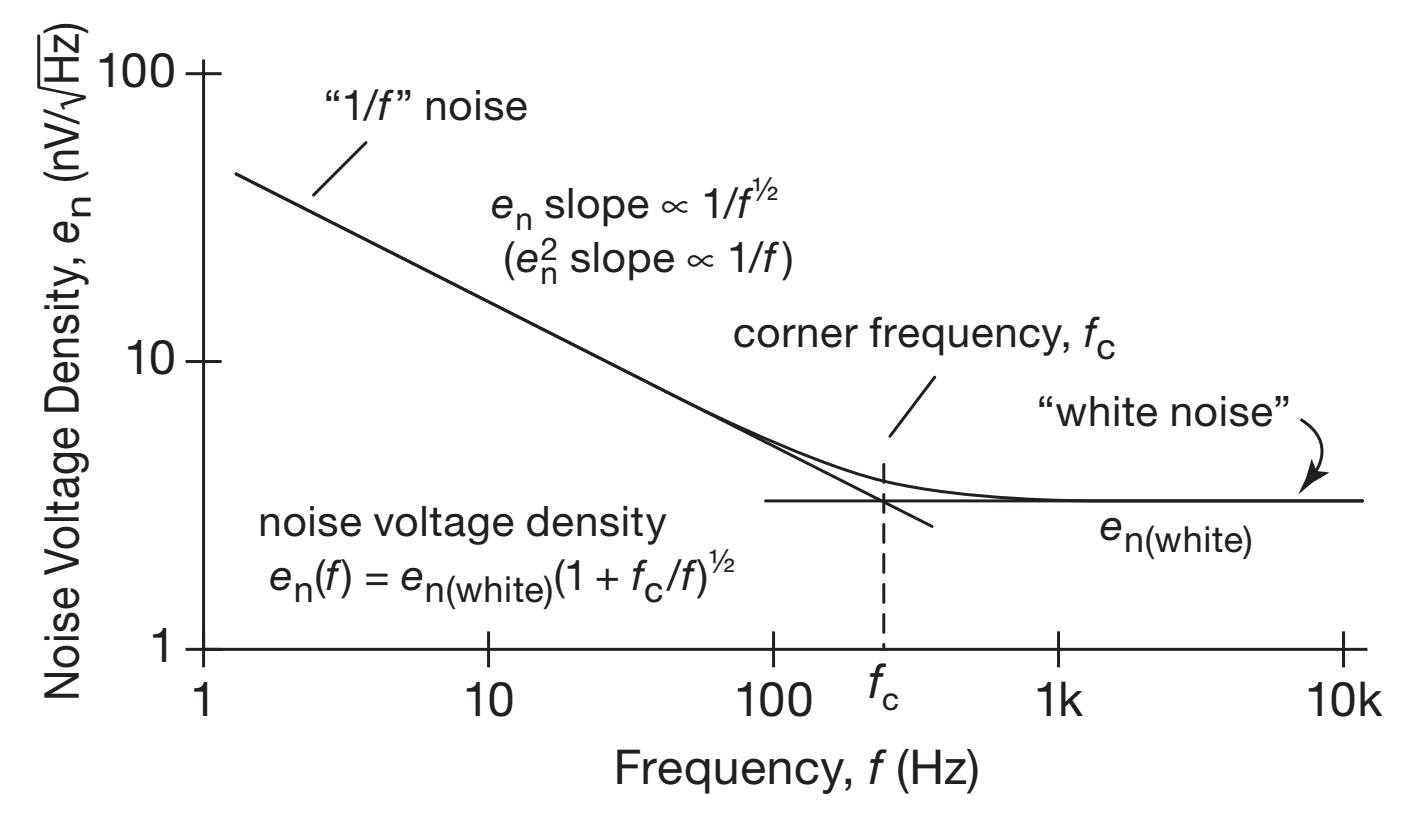
- Ruído 1/f (Flicker), causado por uma infinidade de razões…
Ex.: ruído Johnson-Nyquist
H. Nyquist, Thermal agitation of electric charge in conductors, Phys. Rev. 32, 110 (1928).
- Como compreender o ruído Johnson, devido às excitações térmicas dos portadores de carga num resistor?
- Energia térmica de um portador de carga em 1D a temperatura \(T\): \(\propto kT/2\)
- Potência devido aos portadores numa dada faixa de frequência \(\Delta f\): \(\propto \frac{kT}{\Delta T} = kT \Delta f\)
- Potência associada a uma d.d.p. entre os terminais de um resistor (R): \(v^2/R\)
- Tensão Johnson: \(\frac{v^2}{R}=4 kT \Delta f\), ou \[v_{RMS} = \sqrt{4 k T R \Delta f}\]
- Nota: o fator \(4\) entra devido a uma consideração correta do fluxo de cargas, bem como do teorema da equipartição.
Algumas cores de ruído
- Rede elétrica (60 Hz)
- Costuma estar sempre presente, mesmo tomando-se medidas preventivas.
- Ruído rosa (1/f)
- Várias fontes de ruído operam em frequências baixas em algum momento. Ex.: sismos, correntes de ar, flutuações de temperatura…
- Ruído branco (presente em todas as frequências)
- Shot noise e Johnson. Origem na física fundamental da operação do circuito e estará sempre presente. Tipicamente pode ser considerado pequeno.
Acoplamento AC e ajuste de offset
- Supor \(V_i = V_{i,DC}+V_{i,AC}e^{j\omega t}\). Qual a impedância entre os nós de tensão \(V_i\) e \(V_a\)
- \(Z(\omega = 0) = \frac{-j}{\omega C}\rightarrow \infty\)
- \(Z(\omega = 0)\) equivale a um curto-circuito ou circuito aberto?
- Componente DC do sinal \(V_i\) não “passa” para \(V_a\)
- \(Z(\omega \rightarrow \infty) = \frac{-j}{\omega C} \rightarrow 0\)
- \(Z(\omega \rightarrow \infty)\) equivale a um curto-circuito ou circuito aberto?
- Componente AC do sinal \(V_i\) passa completamente
- Qual é o componente DC de tensão em \(V_a\)?
- \[V_a = \frac{4,7k}{10k + 4,7k} 9V + V_{i,AC}e^{j\omega t}\]
Acoplamento AC e ajuste de offset
- Qual é a tensão em \(V_b\)?
- \[V_b = V_{i,AC}e^{j\omega t}\]
- Acoplamento AC pode ser usado para eliminar alguns tipos de ruídos mais simples em baixa frequência
- Qual é a frequência característica de corte entre \(V_i\) e \(V_a\)?
- \(f_{3dB} = \frac{1}{2\pi R C}\), onde \(R = \left(4,7\,k\Omega\parallel 10\,k\Omega\right)\) e \(C=4,7\,\mu\text{F}\)
Algumas formas de eliminação de ruído
- Diferentes tipos de ruídos requerem estratégias diferentes para sua eliminação
- Ex.: Sinal com frequência bem definida \(f\)
- Passa-baixa, passa-alta, passa-banda ou notch?
- Notar que, caso tenhamos o controle de \(f\), podemos projetar um filtro adequado de forma simples.
- Ex.: como podemos eliminar o ruído em 60 Hz usando um resistor e um capacitor?
- Usando um filtro passa-alta. Qual o menor valor adequado para \(f_{3dB}\)?
- Suponha que o sinal de interesse possui \(f=1\text{ KHz}\). Qual a atenuação do sinal? E do ruído em 60 Hz?
- Relação sinal ruído: compromisso entre passagem do sinal de interesse e ruído resultante. \[\frac{S}{N} = \frac{|T(1\text{ kHz})|}{|T(60\text{ Hz})|} \frac{|v_s|}{|v_N|}\]
Sinais pequenos
- O que fazer se o sinal de interesse é muito pequeno?
- Ex.: supor \(V_1=v_N + v_s\), onde a tensão de ruido \(v_N\) e de sinal \(v_s\) satisfazem \(v_N\gg v_s\).
- Sabemos realizar soma e subtração de tensões
- Se conseguirmos produzir uma tensão \(V_2 = v_N\), onde \(V_2\) inclui todas as fontes de ruído do sistema, exceto o sinal de interesse, então \[v_s = V_1-V_2\]
- Medida do tipo diferencial. Costuma exigir amplificação
- Veremos algumas ideias mais adiante na parte de amplificadores operacionais.
- Nota: Esta ideia também pode ser aplicada para remover o ruído de baixa frequência:
- Pode-se medir a resposta do sistema quando não há sinal, \(V_2=V(t)=v_N(t)\), e depois ativar o sinal para medir \(V_1=V(t+\delta)=v_N(t+\delta)+v_S(t+\delta)\). Em outras palavras, o sinal é uma onda quadrada sobre um padrão de ruído de fundo. Se a modulação é rápida o suficiente, tal que \(v_N(t+\delta)\approx v_N(t)\), temos \[V(t+\delta)-V(t)=v_S(t+\delta)\]