Diodos e circuitos não lineares
FI577 - Instrumentação eletrônica para a física
Leituras recomendadas: Agarwal Caps. 16 e Horowitz & Hill Cap. 1
Diodos e circuitos não lineares
- Até aqui consideramos apenas circuitos contendo elementos lineares
- \(V \propto I\)
- Os efeitos das fontes são independentes
- Thévenin
- Para controlar o comportamento de circuitos, precisamos também de elementos com um comportamento não linear
- \(V = f(I)\), onde \(f(I)\) não é uma função de primeiro grau.
- Os efeitos das fontes não são mais independentes. Podemos obter respostas diferentes, dependendo de cada configuração específica do circuito.
- Não vale Thévenin
- Consideraremos inicialmente o diodo
Junção PN
- Silício é um semicondutor. Conduz pouco em seu estado puro.
- Podemos introduzir no silício cargas livres positivas (dopagem tipo P, p.ex. com fósforo) ou negativas (dopagem tipo N, p. ex. com alumínio)
- Fisicamente, o diodo contém uma região com dopagem P justaposta a uma junção tipo N.
- Assimetria nos portadores de carga em cada terminal
- Assimetria no fluxo de portadores (corrente)
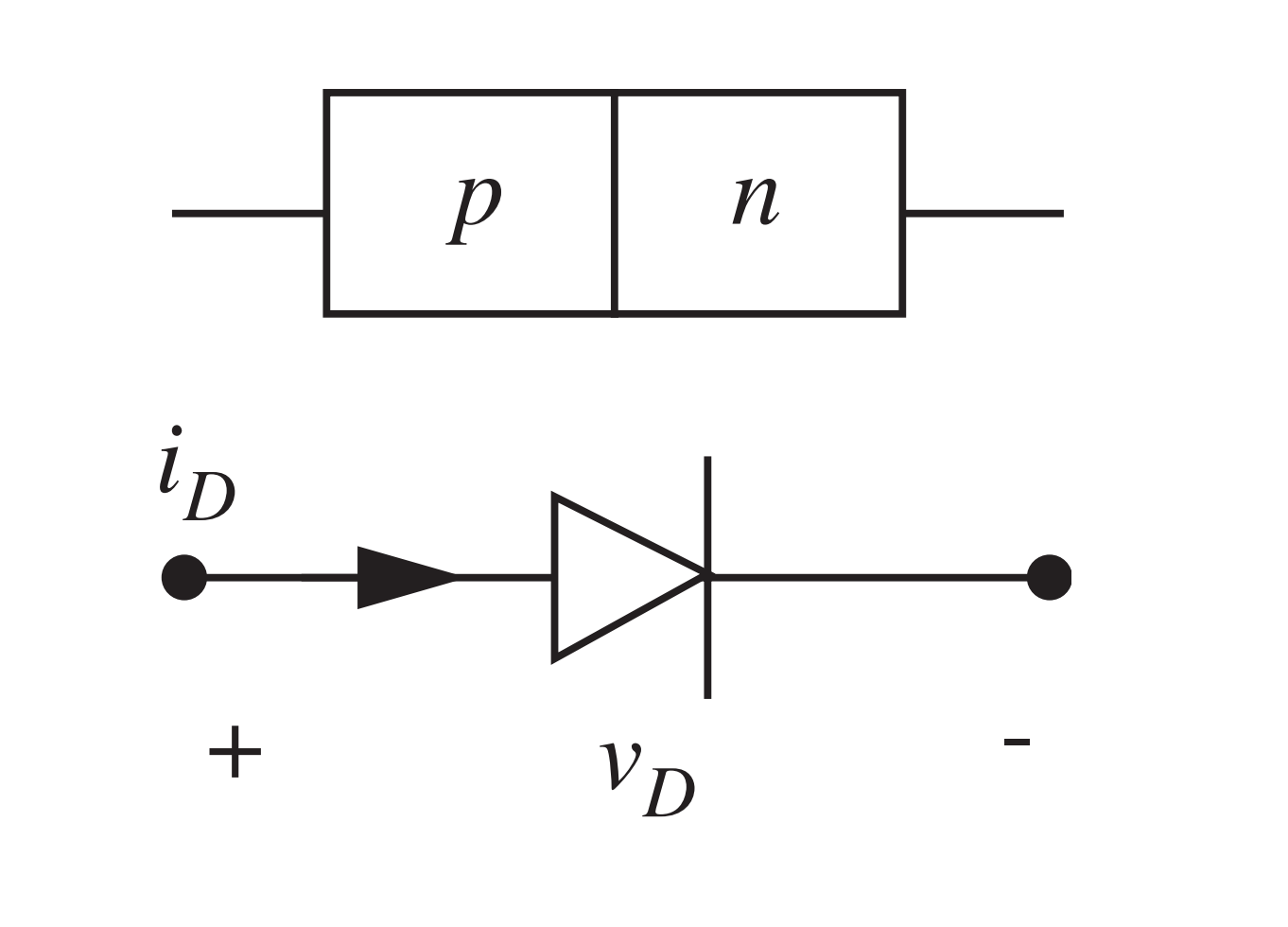
Comportamento do diodo
- Vimos na prática 1 que a corrente só flui entre os terminais do diodo para uma polarização da tensão.
- Polarização direta: tensão mais positiva no terminal P
- Polarização reversa: tensão mais positiva no terminal N
- Alguns conceitos gerais conforme o potencial percebido pelos portadores de carga negativa
- Considere elétrons com energia \(\mu\) (potencial químico)
- Polarização direta: pequeno aumento da d.d.p. entre P e N ‘empurra’ os portadores para a junção.
- Polarização reversa: pequena redução na d.d.p. entre P e N não permite a passagem de corrente devido ao campo elétrico natural da junção.
- Avalanche: grande redução na d.d.p. entre P e N permite a passagem de uma grande corrente
Análise de circuitos contendo elementos não lineares
- Relação \(i\) vs \(v\) para um diodo: \[i = i_s \left(e^{v/v_{th}}-1\right),\] onde \(v_{th}=kT/q\) é a energia térmica \(kT\) de um portador de carga \(q\). \(i_s~1\text{ pA}\) e \(v_{th}~0.025\text{ V}\)
- Relação não linear
- Como analisar um circuito contendo elementos não lineares?
- Várias das simplificações anteriores não são mais válidas…
Uma questão de escala
- Consideremos a curva \(i\) vs \(v\) para um diodo típico em duas escalas distintas.
- \(i = i_s \left(e^{v/v_{th}}\right)\), com \(i_s~1\text{ pA}\) e \(v_{th}~0.025\text{ V}\)
- Na escala de pA, o caráter exponencial é mais evidente
- Na escala de mA, o diodo aparenta um comportamento tipo limiar:
- Não conduz, se \(v<0.6\,\text{V}\)
- Conduz, se \(v>0.6\,\text{V}\)
- Como podemos modelar o comportamento do diodo em termos de elementos mais simples?
Método de estados assumidos
- Podemos considerar o circuito inicial e assumir que o diodo possui 2 estados: circuito fechado ou aberto.
- Diodo ligado: \(v=0\), para qualquer \(i\) positivo.
- Diodo desligado: \(i=0\), para qualquer \(v\) negativo.
- Método:
- Desenhar subcircuito para cada estado do diodo (Lig./Deslig.)
- Analisar o comportamento de cada subcircuito
- Verificar quando as expressões no passo (2) são válidas
Exemplo
- Retificador de meia onda
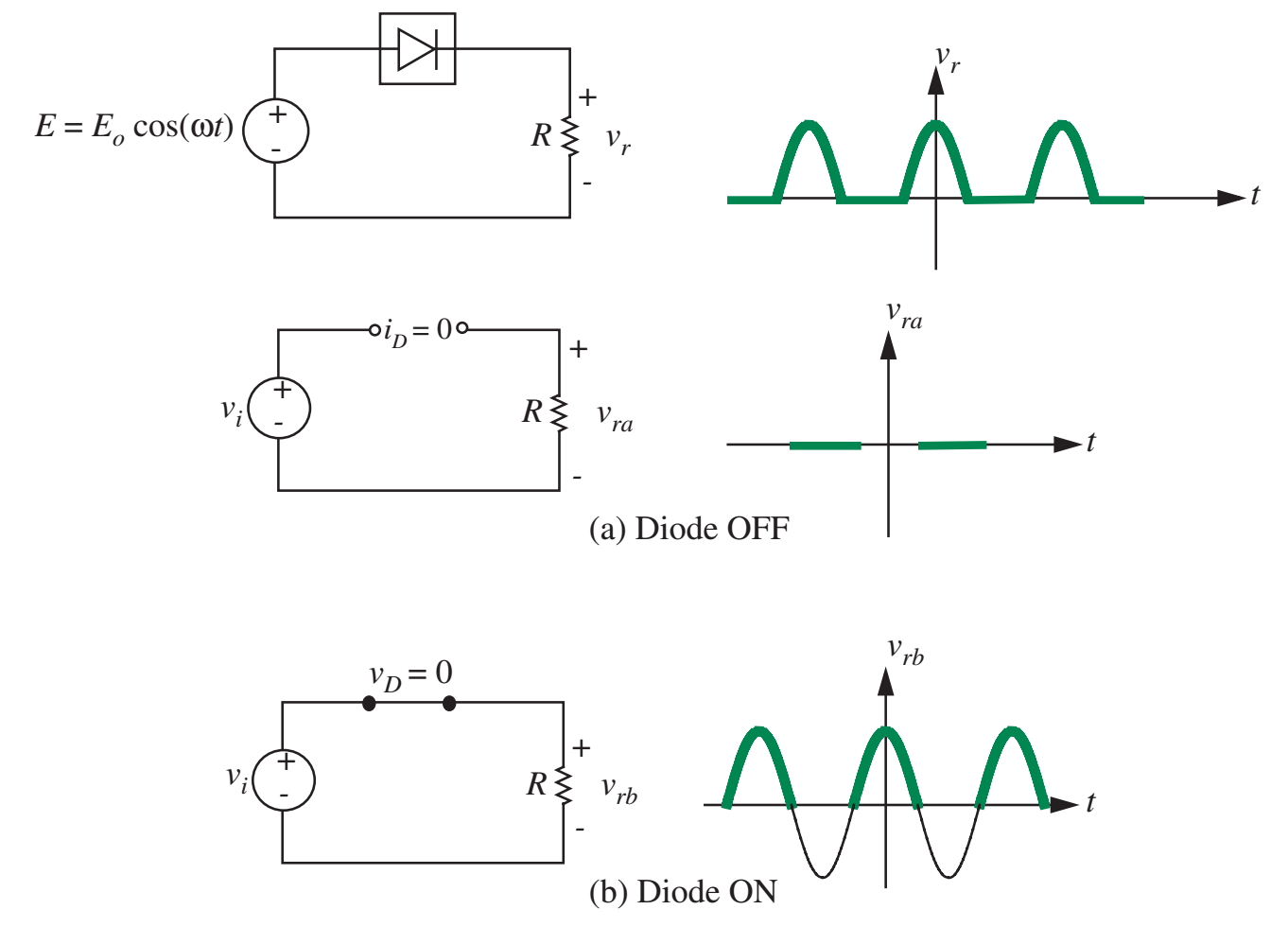
Modelo aprimorado
- Podemos aproximar a curva \(i\) vs \(v\) de forma ainda melhor com os seguintes estados:
- Diodo desligado: \(i=0\), para qualquer \(v<0.6\) negativo.
- Diodo ligado: \(v=0.6+R_D i\), para qualquer \(i\) positivo.

Detector de pico
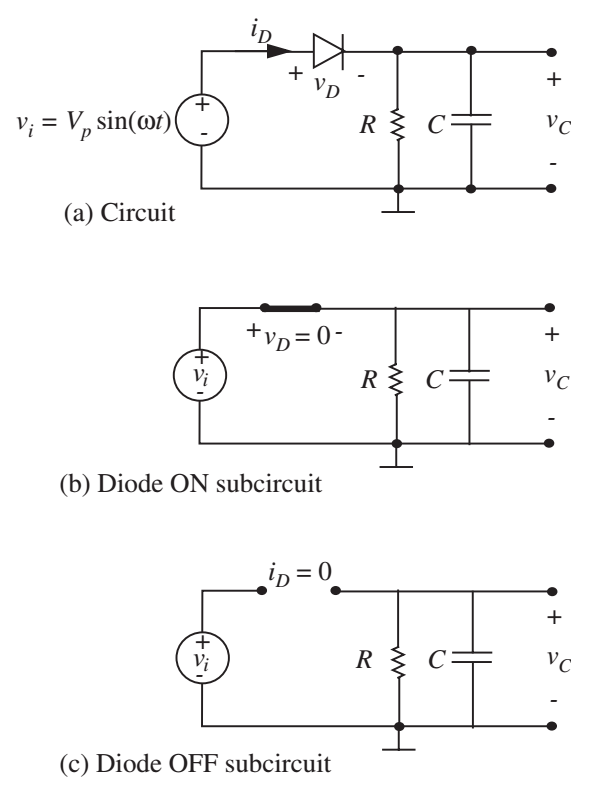
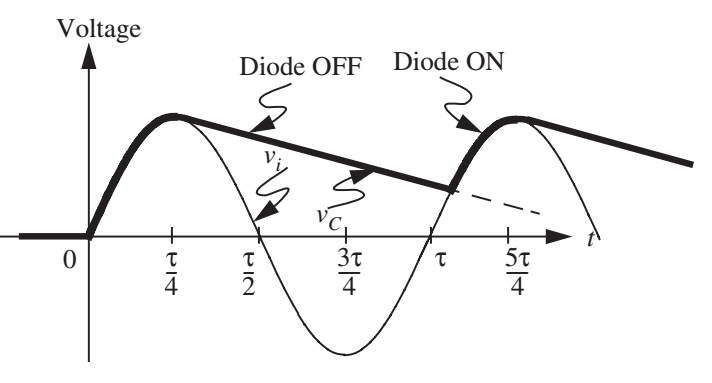
Retificador
- Estimar a flutuação na tensão do capacitor em função do tempo?
- Tensão de ripple (oscilação) pico-a-pico \(\approx V_p \frac{\tau}{RC}\)
- Importante ao considerar fontes de tensão retificadas.
- Se \(RC~10\tau\), a oscilação na tensão é ~\(10\%\)