Introdução

• Até o momento não falamos muito a respeito do comportamento dinâmico dos circuitos
• No entanto, o tempo está presente em tudo o que fazemos
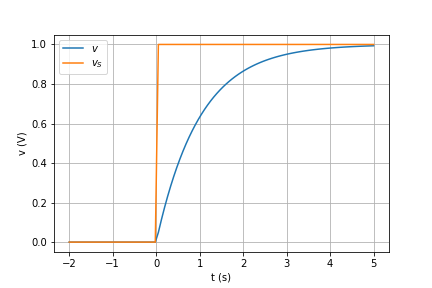
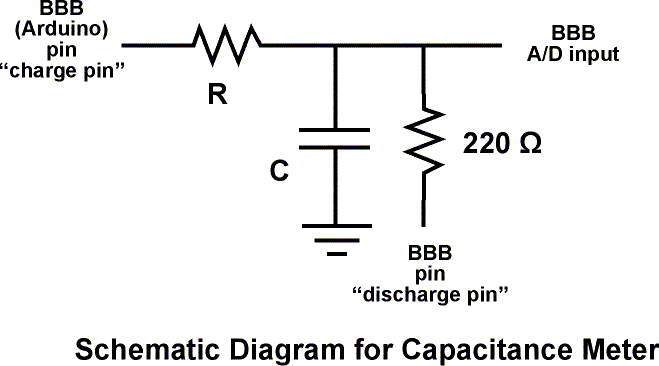
• O circuito mais simples em que podemos analisar detalhadamente seu comportamento é o circuito RC (Resistor-Capacitor)

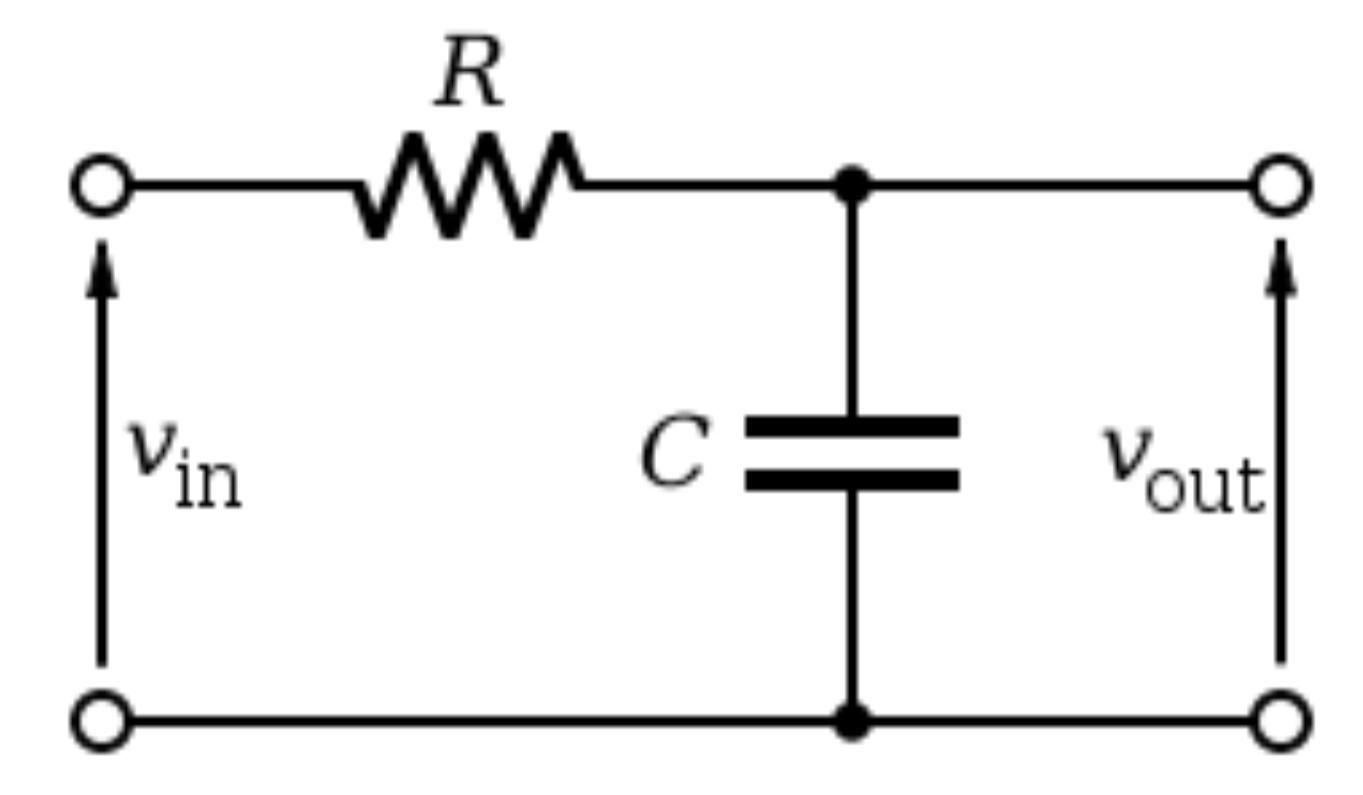
Circuito RC

Descrição matemática

Circuito RC

• Tensão aplicada: \(V_S\)
• Tensão no Capacitor: \(q=Cv\)
• Tensão no resistor: \(v_S-v = R i\)
• Problema: Como encontrar \(v\), se \(V_S\) varia no tempo?

Solução: montar uma equação diferencial

• Temos que \(q=Cv\) e \(\frac{v_S-v}{R} = i\)
• Lembrando, \(i\) indica quanta carga flui pelo fio por unidade de tempo (C/s), podemos usar que \(i=\frac{dq}{dt}\)
• Daí, \(q = Cv\), ou \(\frac{dq}{dt} = i = C\frac{dv}{dt}\)
• Então, \(\frac{v_S-v}{R}=C\frac{dv}{dt}\), ou passando \(v\) para um mesmo lado da eq.,
• \[RC\frac{dv}{dt} + v = V_S\]
• Agora só precisamos resolver a equação diferencial

Solução homogênea (\(V_S=0\))

\[RC\frac{dv}{dt} + v = V_S\]

• A solução mais simples para a Eq. Dif. ocorre quanto \(V_S=0\)
• Note então que \(RC\frac{dv}{dt} + v = 0\), ou \(\frac{dv}{dt} =-\frac{1}{RC}v\).
• Que função é proporcional a sua derivada?
• \(v\) é uma função tipo exponencial! Podemos verificar de maneira mais rigorosa, caso façamos a integração
• \(\frac{dv}{v}=-\frac{dt}{RC}\) -> Integrando o tempo de \(0\) a \(t\), temos
• \(\log{\frac{v}{v_0}}=-\frac{t}{RC}\), ou então \(v = v_0 e^{-t/RC}\)
• \(\tau = RC\) é conhecido como o tempo de carga/descarga do capacitor
• Notar que \(\lim_{t\rightarrow\infty} v =0\).

Solução inhomogenea (\(V_S\neq 0\))

\[RC\frac{dv}{dt} + v = V_S\]

• Supor \(v = v_0 e^{-t/RC} + v_1\)
• \(\frac{dv}{dt} = -\frac{v_0}{RC} e^{-t/RC}\)
• \(RC\frac{dv}{dt} + v = -RC\frac{v_0}{RC} e^{-t/RC} + v_0 e^{-t/RC} + v_1 = V_S\)
• \(v_1 = V_S\) é solução
• \(v = v_0 e^{-t/RC} + v_S\)

O que acontece quando \(V_S\) liga abruptamente?

• \(v = v_0 e^{-t/RC} + v_S\) é tal que \(v(0)=0\)
• \(0 = v_0 e^0 + v_S\), ou \(v_0 = - v_S\)
• Finalmente, \[v = V_S \left(1- e^{-t/RC}\right)\]

Curva de carga de um capacitor

Gerenciando melhor o tempo do arduino

• Até aqui, quando queriamos controlar o comportamento do arduino, usamos sempre a função delay.
• O problema disto é que o arduino para todas as outras atividades (como comunicação, ler os valores dos pinos,...) enquanto o delay não for executado totalmente.
• Como contornar este problema?
• Usando um relógio, para saber se já é hora de o arduino executar alguma tarefa, ou não.

Blink without delay

• Abrir o exemplo 02.Digital/BlinkWithoutDelay

const int ledPin =  LED_BUILTIN;
int ledState = LOW;
unsigned long previousMillis = 0; // Ultima vez que o millis foi chamado
const long interval = 1000;       // Intervalo para piscar o LED

void setup() {pinMode(ledPin, OUTPUT);}

void loop() {
  unsigned long currentMillis = millis();
  if (currentMillis - previousMillis >= interval) {
    previousMillis = currentMillis; // Ultima vez que o led piscou
    if (ledState == LOW) {
      ledState = HIGH;
    } else {
      ledState = LOW;
    }
    digitalWrite(ledPin, ledState);
  }
}

Exercícios

Carga e descarga de um capacitor

1. Faça um programa que carrega e descarrega um capacitor, conforme o circuito acima. Escolha valores de R e C tal que o tempo característico de carregamento seja longo o suficiente para ser medido (vários ms). Detalhe importante: Para que o capacitor possa ser carregado e descarregado corretamente, é fundamental que o pino de descarregamento esteja como pinMode(pin, INPUT) durante a etapa de carregamento. Caso esteja como OUTPUT, funcionará como uma fonte de tensão de 0V, ou 5V, enquanto que no modo INPUT não passa corrente pelo pino.
2. Meça o tempo \(T\) para que o capacitor carregue 63.2% de sua carga total. (Sugestão: usar a função ou ).
3. Calcule a capacitância, usando que no tempo \(T=RC\) o capacitor atinge \(1-e^{-1}=63.2\%\) da tensão máxima.
4. Uma vez que o tempo de carga depende do valor de \(R\), use diferentes pinos e resistências para controlar o tempo de carga do capacitor. Lembre-se sempre de comparar o valor medido com a especificação, ou uma medida complementar dos componentes usando um multímetro.

Usando um circuito RC para tomar médias

• Um dos aspectos mais interessantes em compreender o aspecto dinâmico dos circuitos é que podemos modificar o comportamento do sistema, e podemos realizar operações mais complexas nos circuitos.
• Por exemplo, o fato de um circuito RC responder mais lentamente do que um sinal de tensão aplicado, indica que podemos usar o circuito RC para tomar médias.
• Isto pode ser aplicado, por exemplo, para converter o sinal PWM (onda quadrada) do analogWrite em uma tensão mais suave
• Veremos isto mais abaixo

Breve descrição matemática

• Sabemos que a tensão no capacitor varia como
• \(v = v_0 e^{-t/RC}\), caso a tensão aplicada seja nula, e
• \(v = V_S \left(1- e^{-t/RC}\right)\) quando se aplica uma tensão \(V_S\) e o capacitor está descarregado.
• O que ocorre quando aplicamos um sinal tipo onda quadrada?
• Onda de amplitude \(V_S\), ligada por um tempo \(T_1\) e período \(T\).

Carregamento do capacitor

• Onda de amplitude \(V_S\), ligada por um tempo \(T_1\) e período \(T\).
• Como a onda está sempre presente, podemos ter uma certa carga média presente no capacitor
• Supomos então que, quando a tensão é \(V_S\), a tensão no capacitor é
• \(v(t<T_1) = V_S \left(1- e^{-t/RC}\right) + v_0 e^{-t/RC}\)

Descarregamento do capacitor

• Entre os tempos \(T_1\) e \(T\), não há tensão aplicada e o capacitor descarregará
• Notem então que \(v(T_1) = V_S \left(1- e^{-T_1/RC}\right) + v_0 e^{-T_1/RC}\)
• \(v(t>T_1) = \left[V_S \left(1- e^{-T_1/RC}\right) + v_0 e^{-T_1/RC}\right]e^{-(t-T_1)/RC}\)
• \(v(T) = \left[V_S \left(1- e^{-T_1/RC}\right) + v_0 e^{-T_1/RC}\right]e^{-(T-T_1)/RC}\)

Condição de periodicidade

• Supondo que a onda está ligada por muito tempo, a resposta do capacitor deve possuir a mesma periodicidade da onda quadrada.
• Então, \(v(T)=v(0)=v_0\), e
• \(v_0 = \left[V_S \left(1- e^{-T_1/RC}\right) + v_0 e^{-T_1/RC}\right]e^{-(T-T_1)/RC}\)
• Rearranjando, obtemos \(v_0 = V_S \frac{e^{T_1/RC}-1}{e^{T/RC}-1}.\)
• Se utilizarmos que para \(x\ll 1\) vale \(e^x\approx 1 + x\), temos que quando \(T_1<T\ll RC\)
• \(v_0 = V_S \frac{T_1}{T}.\)

O que acontece com a tensão no capacitor?

• \(v_0 = V_S \frac{T_1}{T}\) é de certa forma uma tensão média (existe outra maneira mais rigorosa para definir a média)
• No entanto, a tensão no capacitor não é constante. Qual a maior variação na tensão do capacitor?
• \(v(T_1) - v_0 = \Delta v = V_S \left(1- e^{-T_1/RC}\right) - v_0 (1-e^{-T_1/RC})\)
• \(\Delta v = V_S \left(1- e^{-T_1/RC}\right) \left(1-\frac{e^{T_1/RC}-1}{e^{T/RC}-1}\right)\)
• Se \(T_1<T\ll RC\) podemos aproximar as exponenciais novamente como \(e^x\approx 1 + x\), e \[\Delta v = V_S \frac{T}{RC}\frac{T_1}{T}\left(1-\frac{T_1}{T}\right)\]

Variação na tensão

• \(\Delta v = V_S \frac{T}{RC}\frac{T_1}{T}\left(1-\frac{T_1}{T}\right)\)
• Quando a variação é nula?
• Quando a variação é máxima?
• Então, no pior cenário, temos que a tensão varia por \(\Delta v_{max} = V_S \frac{T}{4RC}\). Se \(T\ll RC\), estas flutuações podem se tornar bastante pequenas.
• \(\Delta v_{max}\) indica a incerteza com que conseguimos tomar a média usando o circuito RC.

Exercícios

1. Usando a saída analógica e um filtro RC passa baixa, façam um conversor digital analógico (DAC) para o arduino. Como fica a tensão num osciloscópio? Sugestão: utilize a função analogWrite e teste pares onde \(RC=[1\) s, \(100\) ms, \(10\) ms, \(1\) ms, 100 \(\mu\)s]. O que acontece com \(\Delta v_{max}\) quando \(RC\) varia?
2. Façam com que o sinal devido a média realizada pelo circuito RC produza uma onda triangular.
3. Usando a mesma ideia que no caso anterior, façam um gerador de onda senoidal onde você possa controlar a frequência. Qual a maior frequência que o seu circuito consegue atingir?

Frequências de um sinal

• No encontro anterior, montamos um filtro RC que permitia obter uma média de um sinal. Tomando a média de uma onda quadrada pudemos gerar uma tensão variável em um osciloscópio com vários formatos (onda triangular, senoidal, função constante).
• A grande pergunta neste caso é: quais são as frequências que compõem um dado sinal?
• Vamos supor que o sinal de interesse é periódico, e possui período \(T\).
• Sabemos então que \(v(t)=v(t+T)=v(t+2T)=v(t+3T)\dots\) Após passado um múltiplo inteiro de intervalos de tempo \(T\), o sinal se repete.
• (Detalhe: a análise que faremos a seguir é válida pra "quase tudo" em física! Por razões óbvias, aqui focaremos em eletrônica)

Sinal de período \(T\)

• Sabemos que \(v(t)=v(t+T)=v(t+2T)=v(t+3T)\dots\)
• Que tipo de função matemática seria adequada para representar \(v(t)\)?
• Precisamos de uma função que seja periódica, e tenha período \(T\)...
• Podemos pensar em usar senos e cossenos!
• Mas podemos representar \(v(t)\) em termos de senos e cossenos?

A onda quadrada

• Vamos supor por simplicidade uma onda quadrada de período \(T=1\), e que possui um ciclo de trabalho \(T_{ligado}/T = 50\%\)
• Seno e cosseno de mesmo período: \(\sin(\frac{2\pi}{T} t)\) e \(\cos(\frac{2\pi}{T} t)\)

• 
• A função seno "lembra mais" a onda quadrada ao longo do tempo, mas claramente não descreve bem a onda quadrada perto de \(t=0\). Pode-se fazer algo a respeito?

Melhorando a aproximação da onda quadrada

• Vimos que \(\sin(\frac{2\pi}{T} t)\) tem o mesmo período que a onda quadrada, e representa aproximadamente a onda quadrada.
• Vamos mexer um pouco na função seno para melhorar um pouco a aproximação. Podemos diminuir a amplitude do sinal e deslocar o seno para cima por \(1/2\)

• 
• Notem que depois dos ajustes, temos que \(\frac{1}{2}\sin(2\pi t)+\frac{1}{2}\) possui um termo de frequência \(0\), e outro que possui um período \(T=1 s\).

Melhorando a aproximação da onda quadrada

• Usando as funções seno e cosseno de mesmo período da onda quadrada, \(\sin(\frac{2\pi}{T} t)\) e \(\cos(\frac{2\pi}{T} t)\), modificar a amplitude da oscilação do seno, e adicionar um termo de frequência (período) diferente, melhoramos a aproximação.
• \(\frac{1}{2}\sin(2\pi t)+\frac{1}{2}\) aproxima uma onda quadrada de período \(T\).
• A condição mais importante para um sinal periódico de período \(T\), é que ele satisfaça \(v(t)=v(t+T)=v(t+2T)=v(t+3T)\dots\)
• \(\sin(\frac{2\pi}{T} t)\) e \(\cos(\frac{2\pi}{T} t)\) constituem todas as funções que satisfazem a condição de periodicidade do sinal? Caso haja outras funções, a aproximação pode melhorar...

Melhorando a aproximação da onda quadrada

• Se o seno (ou cosseno) possuir um período menor que \(T\), também é possível satisfazer a condição de periodicidade \(v(t)=v(t+T)=v(t+2T)=v(t+3T)\dots\)
• Notar que após o nosso período completo, \(\sin(\frac{2\pi}{T} T) = \sin(\frac{4\pi}{T} T) = \sin(\frac{6\pi}{T} T)\dots=0\)
• Podemos usar sinais periódicos cujas frequências são \[\omega_k = k \frac{2\pi}{T}\qquad(k\in \mathbb{N}).\] Quanto mais frequências usarmos, melhor ficará a nossa aproximação.
• Os termos que oscilam com uma frequência maior que \(\frac{2\pi}{T}\) são denominadas de harmônicos.

A série de Fourier de uma onda quadrada

• A série de Fourier é representa uma aproximação de um sinal \(v(t)\) de período \(T\) como uma soma de sinais em diferentes frequências
• \(v(t) = \sum_{k=0}^{\infty}\left[a_k \sin(\frac{2\pi k}{T} t) + b_k \cos(\frac{2\pi k}{T} t)\right]\)
• \(a_k\) e \(b_k\) são coeficientes que indicam "quanto" de cada frequência está presente num sinal, bem como a fase relativa de cada frequência.

• Para a onda quadrada, temos \(v(t) = \frac{1}{2} + \frac{2}{\pi} \sum_{k=1}^{\infty} \frac{\sin(2 \pi (2k-1) t)}{2k-1}\) (Ver próximo slide para detalhes)

• 

  Aproximando a onda quadrada por sua série de Fourier

Cálculo dos coeficientes de Fourier \(a_k\) e \(b_k\)

• Para encontrar os coeficientes, vamos usar que \(v(t)\) é conhecido (1, se 0<t<1/2, e 0, se 1/2<t<1), e da propriedade de ortogonalidade entre funções trigonométricas \[\int_0^1\sin(2\pi mx)\sin(2\pi nx) dx = \int_0^1\sin(2\pi mx)\cos(2\pi nx) dx = 0\text{, se }n\neq m\] \[\int_0^1\sin^2(2\pi nx) dx = \int_0^1\cos^2(2\pi nx) = \frac{1}{2} dx\] (Lembrar de cálculo 1!)
• Supondo que é possível realizar a aproximação \[v(t) = \sum_{k=0}^{\infty}\left[a_k \sin(2\pi k t) + b_k \cos(2\pi k t)\right]\], podemos multiplicar a equação em ambos os lados por \(\sin(2\pi nx)\) e integrar \(t\) entre 0 e 1.
• \(\int_0^1 \sin(2\pi n t) v(t) dt = \int_0^1 \sin(2\pi nt) dt \sum_{k=0}^{\infty}\left[a_k \sin(2\pi k t) + b_k \cos(2\pi k t)\right]\)
• \(\int_0^1 \sin(2\pi n t) v(t) = \sum_{k=0}^{\infty}\left[a_k \int_0^1 \sin(2\pi nt)\sin(2\pi k t)dt + b_k \int_0^1 \sin(2\pi nt)\cos(2\pi k t)dt\right]\)
• As integrais envolvendo seno e cosseno são sempre nulas. Já aquelas com produtos entre senos serão todas nulas, exceto para o termo onde \(k=n\).
• \(\int_0^1 \sin(2\pi n t) v(t) dt = \frac{a_n}{2}\)
• Como \(v(t)=1\) apenas quando, 0<t<1/2, \(\int_0^1 \sin(2\pi nx) v(t) dt = \int_0^{1/2} \sin(2\pi nt) dt = \frac{-1}{2\pi n}\left[\cos(\pi n) - \cos(0)\right]\)
• \(\cos(0)=1\), enquanto \(\cos(\pi n) = (-1)^n\). Daí, \(a_n\neq0\) apenas se \(n\) é ímpar, ou \(n=2k-1\), com \(k\in \mathbb{N}\)
• \(a_{2k-1} = \frac{2}{\pi (2k-1)}\). Verifiquem que de fato \(b_n = 0\) para \(n\neq 0\), e que \(b_0=\frac{1}{2}.\)

Frequências da onda quadrada

• Qual a potência do sinal que temos em cada frequência \(\omega_k\)?
• Lembrando que \(v(t) = \sum_{k=0}^{\infty}\left[a_k \sin(\frac{2\pi}{T} t) + b_k \cos(\frac{2\pi}{T} t)\right]\), e \(P = \frac{V^2}{R}\), podemos associar \(a_k^2\) e \(b_k^2\) com a potência média do sinal associado a cada frequência

• 
• Para a maioria das frequências, o sinal não possui qualquer potência. O sinal está distribuído apenas sobre as frequências \(\omega_k = 2\pi(2k-1)\).

Biblioteca tone

• Para gerar sinais com uma frequência bem determinada, o conjunto de funções tone() é bastante útil. Estas funções já estão automaticamente implementadas no arduino.
• Sintaxe: tone(pin, frequency), ou tone(pin, frequency, duration)
• pin: pino utilizado para a saída do sinal de frequência determinada
• frequency: frequência (>31Hz)
• duration(opcional): duração do tempo que a frequência será enviada
• noTone(pin) desativa a geração do sinal
• Ver exemplo em Exemplos\02.Digital\toneKeyboard

Exercicio

1. Pensando em um circuito RC como um divisor de tensão, determine como a resistência efetiva do capacitor varia em função da frequência e da capacitância. Teste capacitores de construção diferente (cerâmico, eletrolítico, polímero, nylon...) e com várias constantes de tempo RC.
2. Gere um sinal de frequência conhecida e, com a ajuda do professor, veja o espectro de frequências no osciloscópio.
3. O que acontece com o espectro de frequências do sinal no osciloscópio quando você
   1. Mede o espectro de potência entre o capacitor e o terra.
   2. Inverte o capacitor e o resistor no circuito e mede o espectro de potência entre o resistor e o terra.