Sensoreamento e controle
Anderson M. Amaral
Aula 1 - Divisor de tensão, botão e LED
Leis de Kirchhoff
- Simplificações algébricas das Eqs. de Maxwell
- Lei das correntes: A soma das correntes que entram em um nó é igual a soma das correntes que saem. A soma das correntes por um nó deve ser nula.
- Lei das tensões: A soma algébrica das tensões dos ramos através de qualquer caminho fechado (laço) em uma rede deve ser nula. A tensão entre dois nós independe do caminho.
- Procedimento de aplicabilidade geral:
- Definir as correntes e tensões em cada ramo de forma consistente. Ex.: usando a convenção de variáveis associadas.
- Considerar as relações constitutivas entre tensão e corrente em cada elemento. Ex.: \(v=ri\)
- Aplicar leis de corrente e tensão de Kirchhoff
- Resolver o sistema de equações resultante
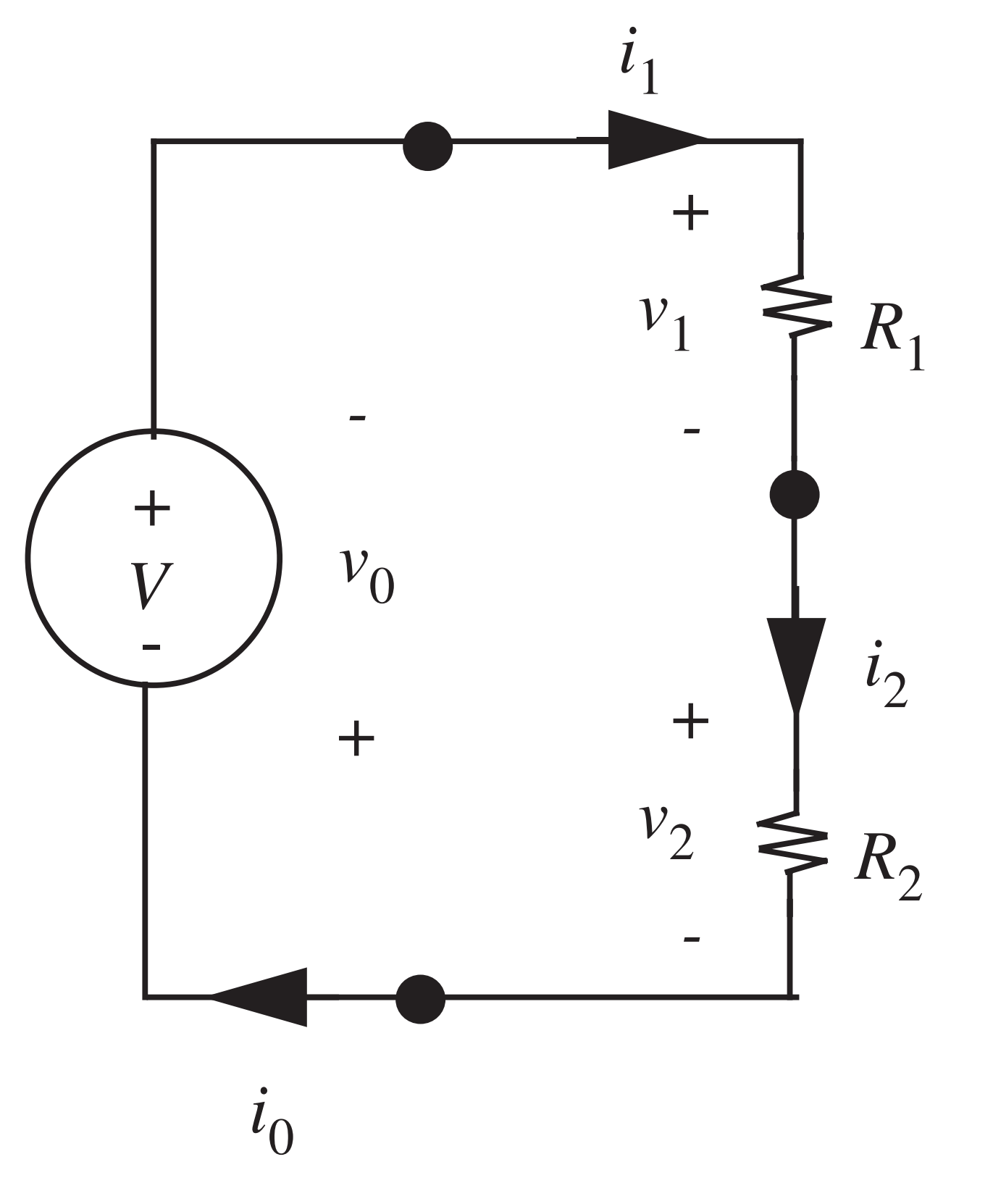
Divisor de tensão
- Um dos tipos de circuitos mais recorrentes é o divisor de tensão
- Temos uma fonte de tensão \(V\), \(v_1=R_1i_1\) e \(v_2=R_2i_2\)
- Kirchhoff:
- Correntes: \(i_0=i_1=i_2\)
- Tensões: \(v_0+v_1+v_2=0\)
- Sol.: \[i_0=i_1=i_2=\frac{1}{R_1+R_2} V,\] e \[v_1=\frac{R_1}{R_1+R_2} V,\] \[v_2=\frac{R_2}{R_1+R_2} V\]
- Note que \(v_2\) é uma fração de \(V\)
Representação elétrica de um botão
- Como representar um botão ideal em um circuito?
- Circuitos aberto (Não há contato elétrico) e fechado (Há contato elétrico).
- Como converter a informação de que o contato elétrico foi realizado ou não em uma tensão?
- Podemos usar um divisor de tensão
- \(V_O = \frac{R_2}{R_1+R_2} V_{CC}\)
- O botão deve ser \(R_1\) ou \(R_2\) para satisfazer as condições acima? O que acontece se trocarmos o resistor e o botão no circuito?
- 2 estados representáveis por uma resistência efetiva:
- Aberto (\(R=\infty\)) queremos que \(V\rightarrow 0\) V
- Fechado (\(R=0\)) queremos que \(V\rightarrow 5\) V
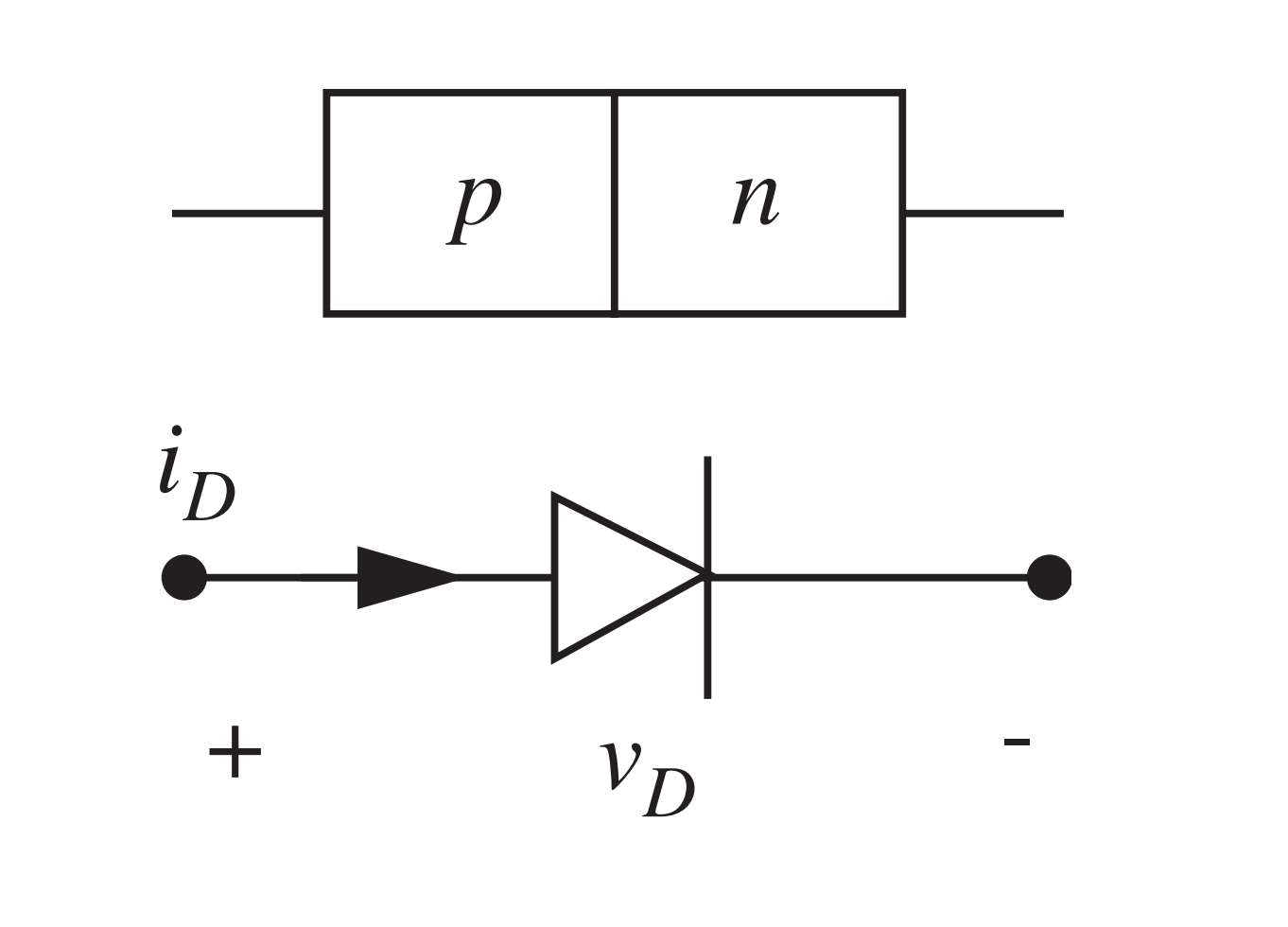
O LED é um diodo
- Idealmente, pode-se representar o diodo usando 2 estados: circuito fechado ou aberto.
- Diodo ligado: \(v=0\), para qualquer \(i\) positivo.
- Diodo desligado: \(i=0\), para qualquer \(v\) negativo.
- Terminais não equivalentes:
+(Anodo) e-(Cátodos)