Sensoreamento e controle
Anderson M. Amaral
Aula 6 - Carga e descarga de um capacitor
Resposta transiente: circuito RC
- Ao aplicar uma tensão num circuito, nem todos os pontos respondem instantaneamente
- Exemplo: circuito RC
![]()
Descrição matemática
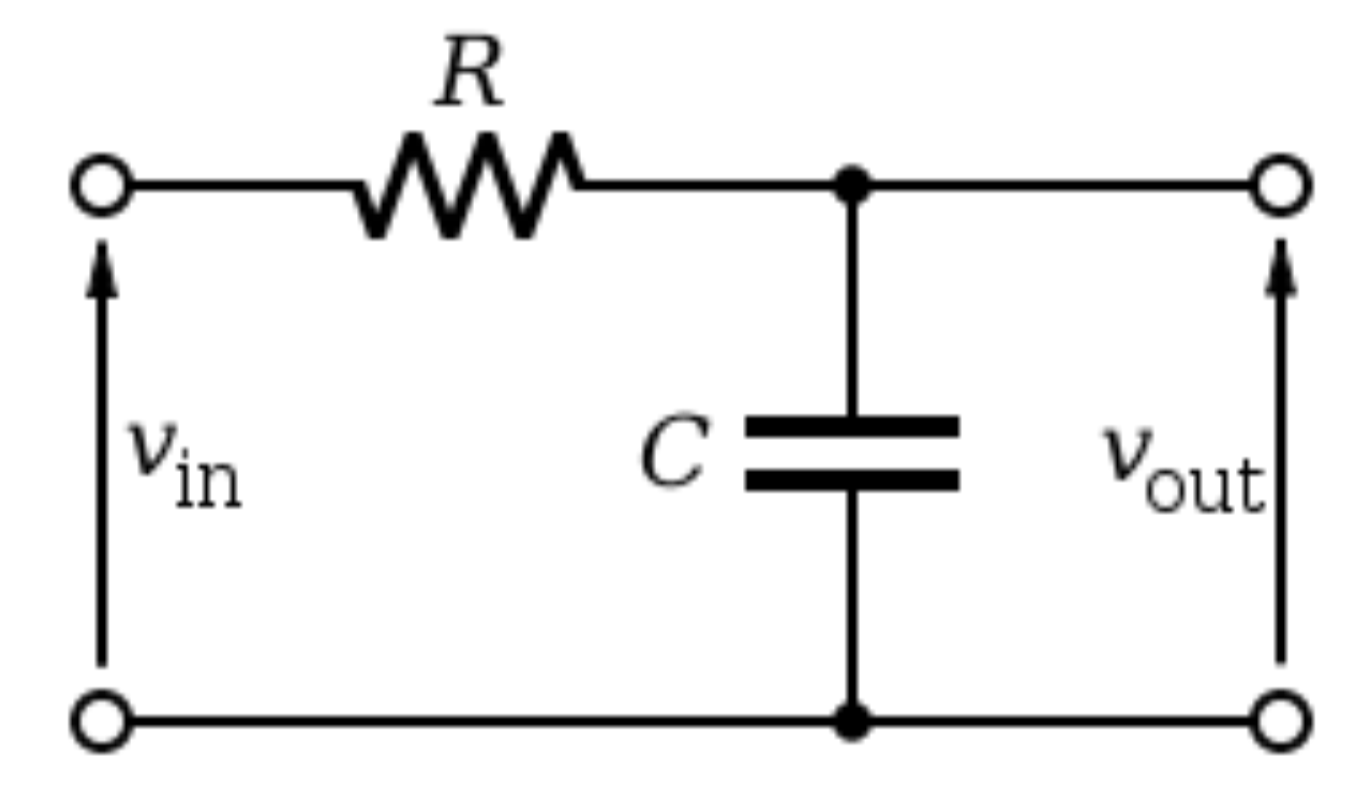
- Tensão aplicada: \(V_S\)
- Tensão no capacitor: \(q=Cv\)
- Tensão no resistor: \(v_S-v = R i\)
- A carga armazenada no capacitor depende de \(i\)!
- A solução matemática depende de uma equação diferencial. \(v\) é dado por exponenciais
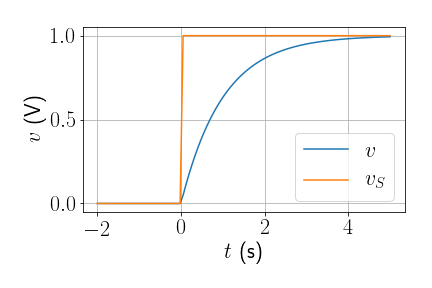
O que acontece quando \(V_S\) liga abruptamente?
- \(v = V_S \left(1- e^{-t/RC}\right)\)
- A demonstração matemática deste resultado pode ser encontrada nos slides mais adiante
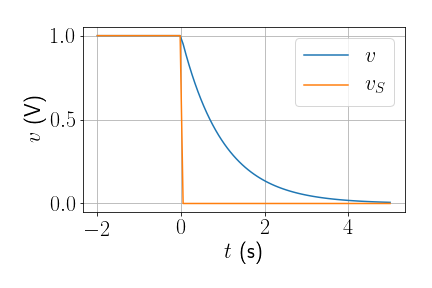
O que acontece quando \(V_S\) desliga abruptamente?
- \(v = V_S \left(e^{-t/RC}\right)\)
- A demonstração matemática deste resultado pode ser encontrada nos slides mais adiante
Demonstração: montando uma equação diferencial
- Temos que \(q=Cv\) e \(\frac{v_S-v}{R} = i\)
- Lembrando, \(i\) indica quanta carga flui pelo fio por unidade de tempo (C/s), podemos usar que \(i=\frac{dq}{dt}\)
- Daí, \(q = Cv\), ou \(\frac{dq}{dt} = i = C\frac{dv}{dt}\)
- Então, \(\frac{v_S-v}{R}=C\frac{dv}{dt}\), ou passando \(v\) para um mesmo lado da eq.,
- \[RC\frac{dv}{dt} + v = V_S\]
- Agora só precisamos resolver a equação diferencial
Solução homogênea (\(V_S=0\))
\[RC\frac{dv}{dt} + v = V_S\]
- A solução mais simples para a Eq. Dif. ocorre quanto \(V_S=0\)
- Note então que \(RC\frac{dv}{dt} + v = 0\), ou \(\frac{dv}{dt} =-\frac{1}{RC}v\).
- Que função é proporcional a sua derivada?
- \(v\) é uma função tipo exponencial! Podemos verificar de maneira mais rigorosa, caso façamos a integração
- \(\frac{dv}{v}=-\frac{dt}{RC}\) -> Integrando o tempo de \(0\) a \(t\), temos
- \(\log{\frac{v}{v_0}}=-\frac{t}{RC}\), ou então \(v = v_0 e^{-t/RC}\)
- \(\tau = RC\) é conhecido como o tempo de carga/descarga do capacitor, ou tempo característico do circuito
- Notar que \(\lim_{t\rightarrow\infty} v =0\).
Solução inhomogenea (\(V_S\neq 0\))
\[RC\frac{dv}{dt} + v = V_S\]
- Supor \(v = v_0 e^{-t/RC} + v_1\)
- \(\frac{dv}{dt} = -\frac{v_0}{RC} e^{-t/RC}\)
- \(RC\frac{dv}{dt} + v = -RC\frac{v_0}{RC} e^{-t/RC} + v_0 e^{-t/RC} + v_1 = V_S\)
- \(v_1 = V_S\) é solução
- \(v = v_0 e^{-t/RC} + v_S\)
O que acontece quando \(V_S\) liga abruptamente?
- \(v = v_0 e^{-t/RC} + v_S\) é tal que \(v(0)=0\)
- \(0 = v_0 e^0 + v_S\), ou \(v_0 = - v_S\)
- Finalmente, \[v = V_S \left(1- e^{-t/RC}\right)\]

O que acontece quando \(V_S\) desliga abruptamente?
- Supondo que a fonte de tensão \(v_S\) está ligada a muito tempo, e é desligada em \(t=0\), quem são \(v(t=0^-)\) e \(v(t\rightarrow\infty)\)?
- \(v = a e^{-t/RC} + b\) é tal que \(v(0)=v_S\) e \(v(\infty)=0\)
- \(v_S = a + b\), e \(0 = b\)
- Finalmente, \[v = V_S \left(e^{-t/RC}\right)\]

Análise intuitiva
- Podemos analisar o que ocorre com o circuito RC em tempos curtos e longos.
- \(v = a e^{-t/RC} + b\)
- \(t \leq 0\)
- \(v_0 = a + b\)
- \(t \gg RC\)
- \(v_\infty = b\)
- \(v = v_0 e^{-t/RC} + v_\infty (1-e^{-t/RC})\)